再帰アルゴリズム その2
再帰アルゴリズムの覚え書きの続きです。
今回も、非効率的かつ非現実的な例題を利用して再帰アルゴリズムを理解していきましょう。
今回はフィボナッチ数列の特定項の値を求めるプログラムです。
フィボナッチ数列とは簡単に説明すると
F1 = 1
F2 = 1
F3 = 2
・
・
・
Fn = F(n – 2) + F(n – 1)
ただし、n = 1 または n = 2 のとき F(n) = 1 となる数列のことである。
つまり、1, 1, 2, 3, 5, 8, … と続く数列で、 隣り合う2つの数を足し算すると、その上位の数になる数列です。
参考までに、フィボナッチ数は、ちょうど800年前に刊行された「算盤の書」(1202年)の中の有名な「兎の問題」から生まれました。
これをプログラムにするにはどうしたらいいでしょうか?
数学的手法でいくか?ループ文で和を取り値を入れ替えながら?
面倒なのでここは再帰アルゴリズムを使いましょう。(^_^;
計算処理負荷が非常に大きいことは秘密にしておきましょう。(ヲヒ
とりあえずサクッと作ってみたのでデバッグ実行させてプログラムの流れを確認してみましょう。
| jp\yucchi.fibonacci.number.FibonacciNumber.java |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
package jp.yucchi.fibonacci.number; /** * * @author Yucchi */ public class FibonacciNumber { private static final int TARGET = 5; private static int ans; public static void main(String[] args) { ans = fib(TARGET); System.out.println("フィボナッチ数列第 " + TARGET + " は " + ans + " です。"); } private static int fib(int n) { if (n == 1 || n == 2) { return 1; } else { ans = fib(n - 2) + fib(n - 1); return ans; } } } |
上記のプログラムをデバッグ実行させます。
変数、n , ans の値、再帰呼び出し及び処理から戻ってくる時のプログラムの流れをしっかり確認してくださいませ。
しっかり確認できましたでしょうか?
概略図を作って流れを考察してみます。
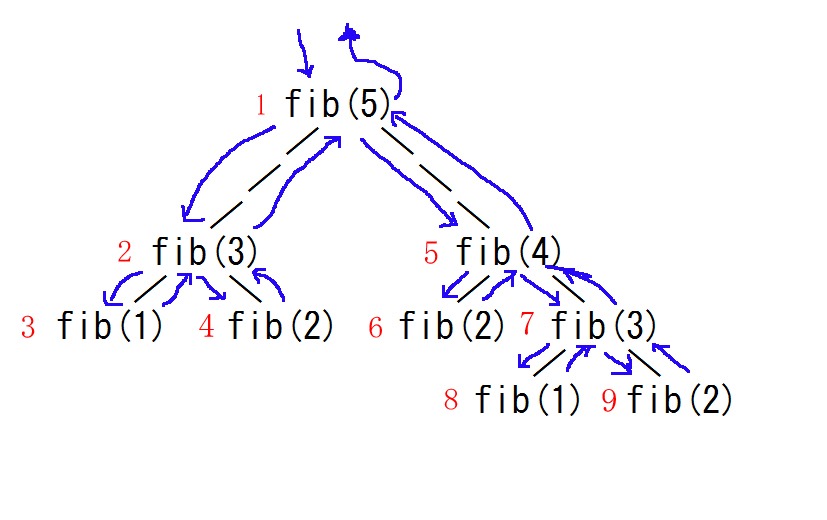
fib(5) から fib(5 – 2) そして fib(3 – 2)
処理を終え fib(5 – 2) に戻り次の fib(3 –1)
処理を終え fib(5 – 2) に戻り fib(5 – 2) の処理を終え fib(5) に戻る
そして fib(5 –1) へ、そして fib(4 – 2) へ、処理を終えて fib(5 – 1) へ戻る
次の fib(4 – 1) へ、そして fib(3 – 2) へ、処理を終えて fib(4 – 1) へ戻る
そして fib(3 – 1) へ、処理を終えて fib(4 – 1) へ戻る、処理を終えて fib(5 – 1) へ戻る、処理を終えて fib(5) に戻る
これでやっと呼び出し元に計算処理を結果を返せるって仕組みです。
あ~、しんど (~_~;)
再帰アルゴリズムってプログラムだとシンプルだけど流れを考えるとしんどいですね。
えっ?私だけ?
まぁ、いいか。
ちなみに再帰アルゴリズム使わないプログラムは下記のようになります。
| jp.yucchi.fibonacci.number2.FibonacciNumber2.java |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
package jp.yucchi.fibonacci.number2; /** * * @author Yucchi */ public class FibonacciNumber2 { private static final int TARGET = 5; public static void main(String[] args) { System.out.println("フィボナッチ数列第 " + TARGET + " は " + fib(TARGET) + " です。"); } private static int fib(int n) { int x = 1; int y = 1; for (int i = 2; i < TARGET; i++) { int z = x + y; y = x; x = z; } return x; } } |
さて、どちらが効率いいですか?
TAGS: Java | 2013年1月2日4:56 AM | Comments : 4

