ユークリッドの互除法 Euclidean Algorithm
Java でユークリッドの互除法 Euclidean Algorithm をプログラミングしてみました。
再帰アルゴリズムを使ってます。
再帰アルゴリズムについてはこちらで簡単な覚え書きを残してあります。
ユークリッドの互除法とはいったいどんな仕組みなのか調べてみました。
ある二つの自然数の最大公約数を求めるのに非常に優れた方法らしいです。
名前に互除法とあるとおり互いに割り算を行って解を導き出す方法です。
簡単に説明すると自然数 r1 と r 2 ( r1 >= r2 ) の最大公約数を求めるとき ( 注意 : r の後の数字と n は小さい数字だと思ってください。)
r1 / r2 の余り r3 を求める。
次に r2 / r3 の余り r4 を・・・
これを rn が 0 になるまで繰り返す。
この時、 r(n-1) が最大公約数となる。
実にシンプルです。
数学的証明はここでは割愛させていただきます。
これを Java プログラムにするには再帰アルゴリズムを使えば簡単にできそうですね。
さっそく作ってみましょう。
| euclidean_algorithm.Euclidean_Algorithm.java |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
package euclidean_algorithm; /** * * @author Yucchi */ public class Euclidean_Algorithm { public static void main(String[] args) { if (args.length != 2) { System.err.println("えらー (゜´Д`゜) 自然数を二つ入力してね。"); System.exit(0); } int x = java.lang.Integer.parseInt(args[0]); int y = java.lang.Integer.parseInt(args[1]); if (x < 0 || y < 0) { System.err.println("えらー (゜´Д`゜) 自然数を二つ入力してね。"); System.exit(0); } if (x < y) { y ^= x; x ^= y; y ^= x; } System.out.println(args[0] + " と " + args[1] + " の最大公約数は " + gcd(x, y) + " だよね。"); } private static int gcd(int x, int y) { return y == 0 ? x : gcd(y, x % y); } } |
非常にシンプルで解りやすいですね。
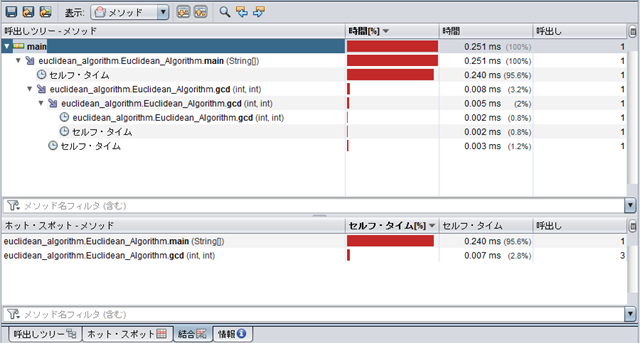
せっかくだからデバッグ実行させてプルグラムの流れを確認してみよう。
変数 x , y の値に注目です。
main() メソッドの引数二つを整数とし、大きさを比較し計算処理のため必要に応じて値を入れ替え、
再帰メソッドで答えが出るまで(再帰のループから抜ける条件になるまで)ひたすらぐるぐる回るってかんじ。
ユークリッドの互除法ってシンプルだけど良く考えられた素晴らしいものですね。
最後にすでにお気付きの方もいると思うのですが上記プログラムはちょっと手抜きの部分があります。
目的がユークリッドの互除法を試してみるということなのでご容赦のほどを(^_^;
ちなみに java.lang.NumberFormatException が・・・・・・です。(本当は忘れていたことは内緒です)
TAGS: Java | 2013年1月3日4:58 AM | Comments : 2