ゆっちのBlog

2012

Solaris 11 インストール vol.2

Solaris

Solaris 11 インストール後にやっておきたいことをいろいろとφ(．．)メモメモ

とりあえず root でログインできるようにします。

まず一般ユーザーでログインします。

次にスーパーユーザーになります。

ロール変更コマンドを打ち込みます。

ロールが変更されたら次のようなメッセージが表示されます。

ではログアウトして root でログインできるか確認します。

やったね！

無事にロール変更して root でログインできるようになりました。

良い子のみんなは決して真似をしないようにね(*^▽^*)

Hatena タグ: Solaris

TAGS: Solaris | 2012年7月25日4:28 AM | Comment : 0

Solaris 11 インストール

Solaris

今更だけど Solaris 11 のインストールの自分用φ(．．)メモメモ

Oracle のサイトより Solaris 11 の ISO ファイルをダウンロードして CD に焼きます。

Text Install を選んでインストールしてみました。

CD ブートしてインストールを開始します。

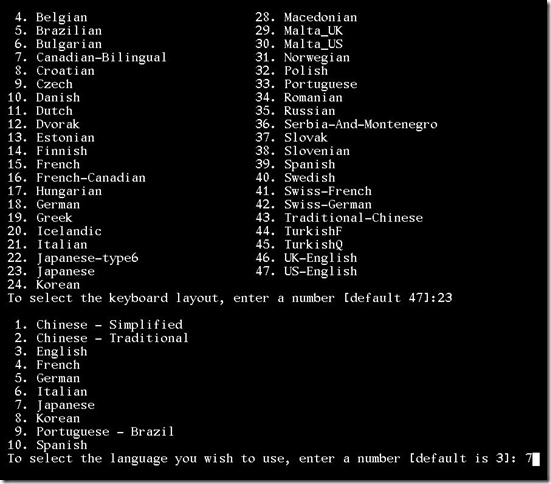
CD-ROM から起動するとキーボードの選択画面が表示されるので 23 を入力します。

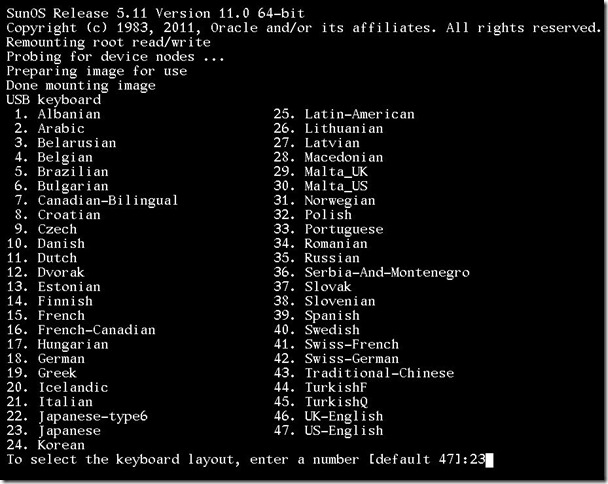
次に言語の選択をします。日本語は 7 ですね。

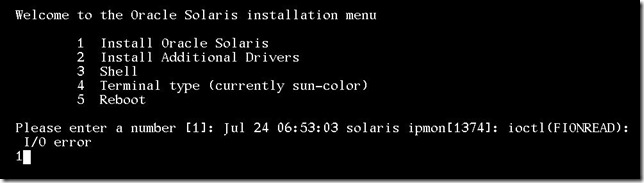
次は Solaris のインストールを選択します。

なにやらエラーが出てますが見なかったことにして 1 を入力します。

そうするとウェルカムスクリーンが表示されますので F2 キーを押します。

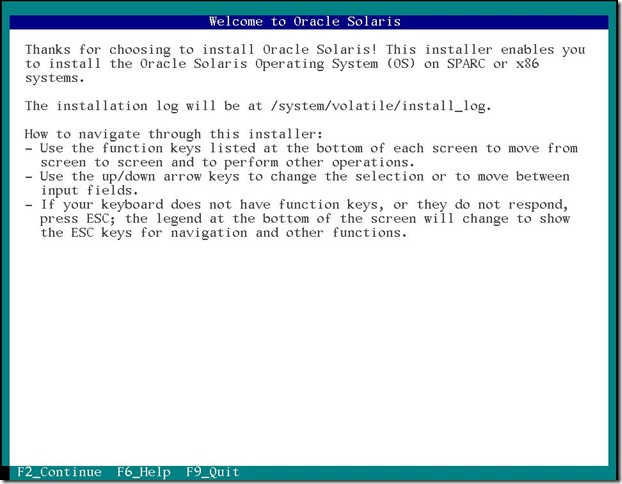
次はインストールするハードディスクの指定です。

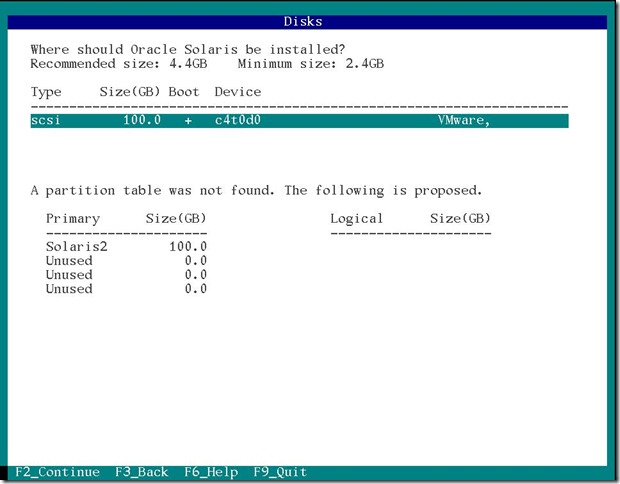
100GB まるまる使うことにしました。

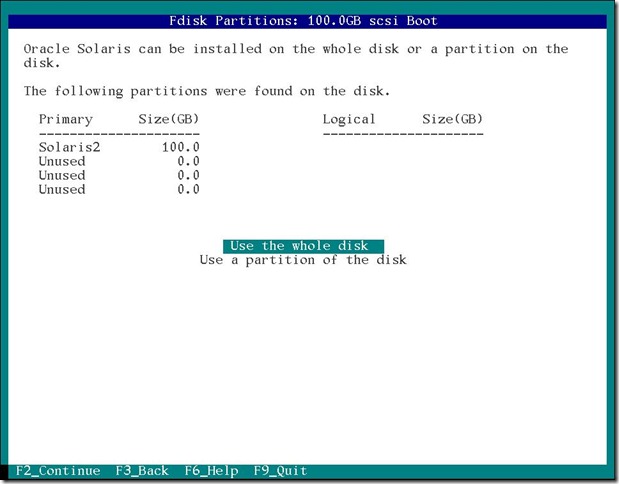
次はネットワーク設定です。

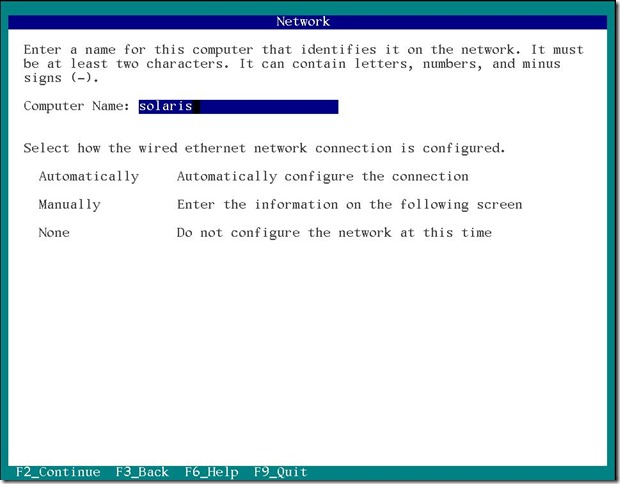
オートマチックを選んで F2 キーを押します。

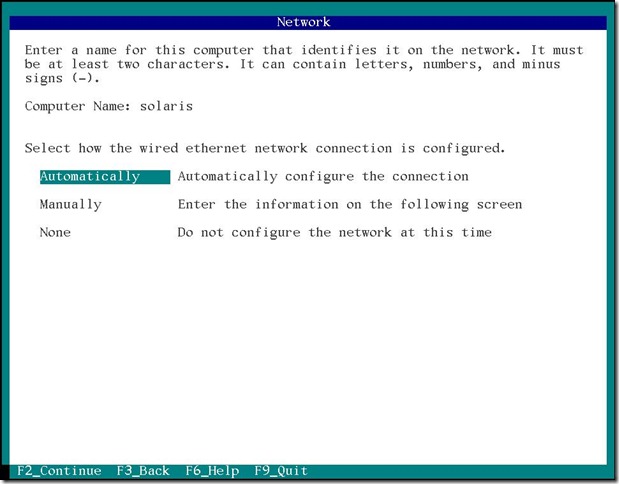
次はタイムゾーン日付時刻の設定です。

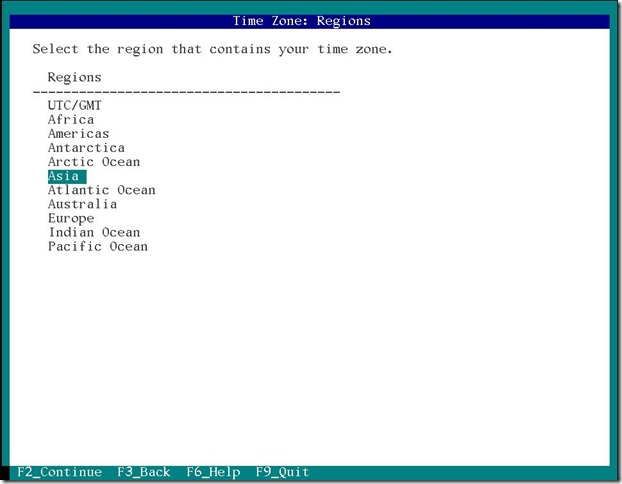
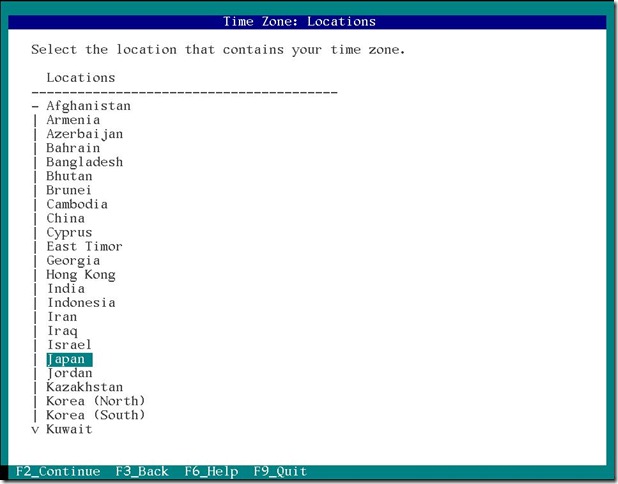
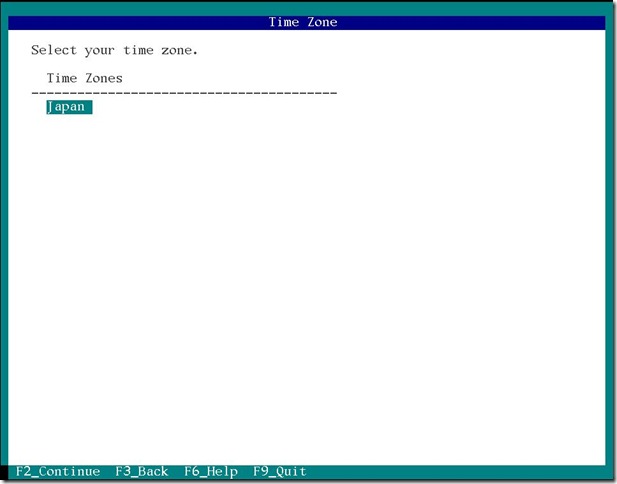
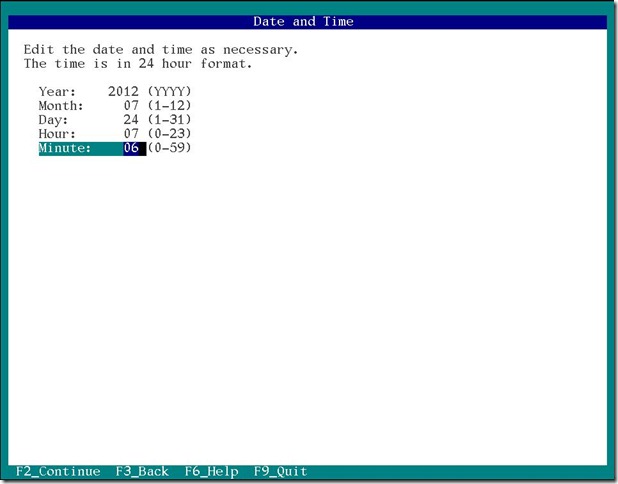
タイムゾーン日付時刻の設定が終わったら次はユーザー設定です。

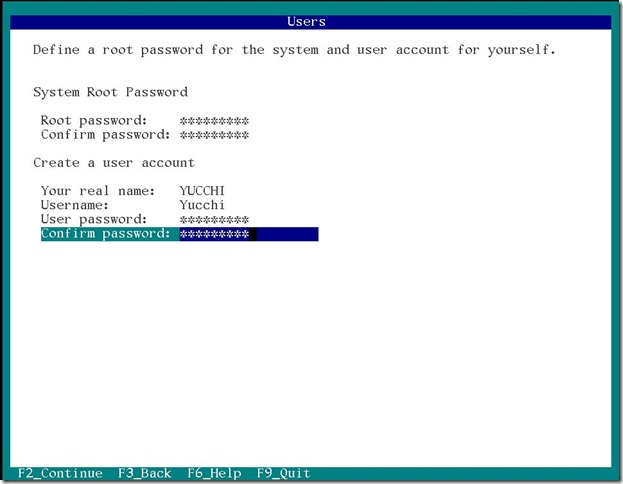
システム管理者 root のパスワードを設定します。

ユーザーアカウントを作成します。

これらは忘れないように秘密の手帳にでもメモしておきましょう。

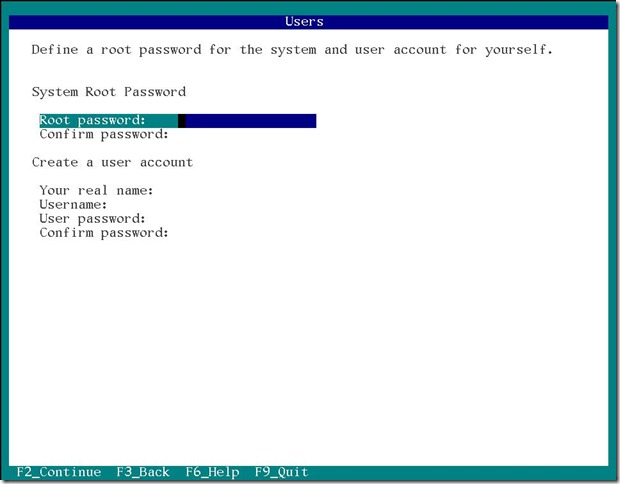
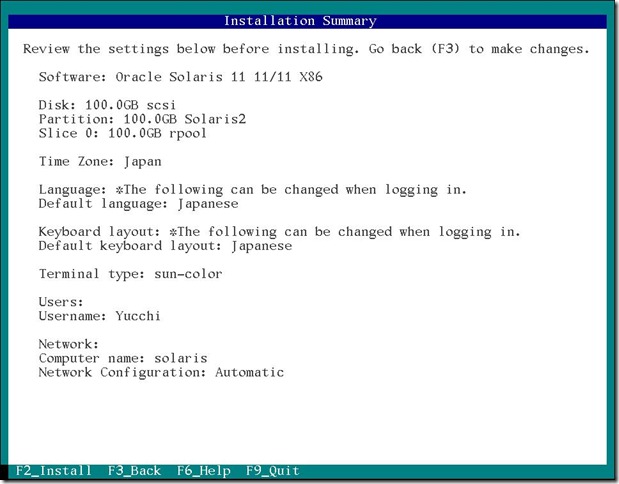
今までの設定情報が表示されますので間違いがないか確認し、よければ F2 キーを押してインストールを開始します。

インストールが開始されますので暇になります。

コーヒータイムでゆっくりくつろぎながら待ちましょう。

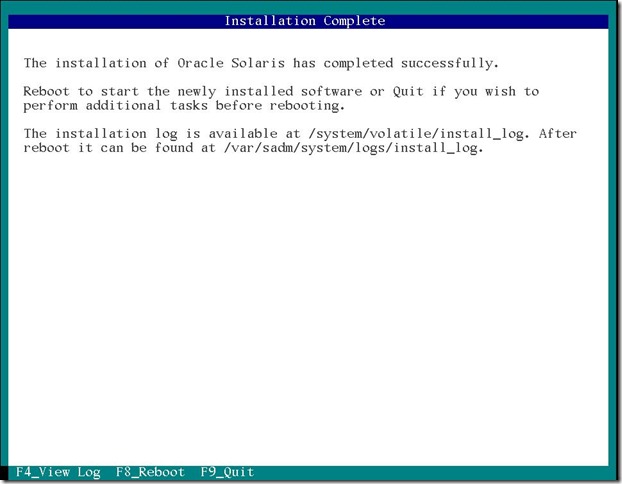
インストールの完了画面がでたら F8 キーを押してリブートします。

無事にインストールされていれば次のような画面がスクリーンに映し出されます。

起動します。

そして root でログインしてみます。

あららら・・・

そういえばデフォルトでは root でログインできないんでしたね。（；´Д｀）

このロールの変更及び、インストール後にやっておきたいことはまた今度ってことで(・_・)(._.)

Hatena タグ: Solaris

TAGS: Solaris | 2012年7月24日2:45 PM | Comment : 0

素数を求める vol.4 （おまけ）

Java

素数を求めるプログラムを作って処理時間を比較したけど

一番最初に作ったもので同様に素数の総数を検出し、表示させるだけの処理時間を計測した。

実行結果は次のようになった。

run:
105097564個の素数を検出しました。
87時間32分8秒6746568970265798
構築成功 (合計時間: 5,252 分 13 秒)

とてつもなく時間がかかりました。(°°;)

以上、おまけでした。

Hatena タグ: Java

TAGS: Java | 2012年7月24日1:32 PM | Comment : 0

素数を求める vol.3

Java

素数を求めるプログラムをシンプルな方法で作ってきました。

総当たり方式のものをシングルスレッドとマルチスレッドのプログラムで。

３億までの素数を検出表示させるプログラムです。

実行結果はシングルスレッドのものが約４時間半、

マルチスレッドのものが約１時間半でした。

ここで最終兵器の登場です。

エラトステネスの篩

これはどういったものかと言うと素数の性質を利用して次々と篩い落としていく感じのものです。

例えば 20 までの素数を求める場合

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

最初の 1 は素数の定義から外れるので素数ではない。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

次の 2 は当然素数の最小値である。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

と言うことは 2 の倍数である 4 6 8 10 12 14 16 18 20 は素数ではない！

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

次の 3 は消されてないから（1 と自分自身の 3 しか割り切れないから）素数である。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

同様に 3 の倍数は素数では無いので消していく。9 と 15 は素数ではない。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

次に現れる 5 は３番目の素数となる。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

同様に 5 の倍数を消していく。と言っても 5 の倍数は残ってない。

ここで 20 までと言う条件から 5 は 20 の平方根より大きいのでこれで終了になり、

残りの 7 11 13 17 19 は素数となる。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

実にシンプルで解りやすいですね。

これをプログラムにすればいいだけです。

私が最終兵器と言ったのは処理速度が先の二つのプログラムのものより異常に速いからです。

結果から先に紹介すると３億までの素数を求めるのに１時間もかからないんです。

run:
2 is Prime Number. —> 1
3 is Prime Number. —> 2
5 is Prime Number. —> 3
7 is Prime Number. —> 4
11 is Prime Number. —> 5

　　　　　略

299999939 is Prime Number. —> 16252323
299999957 is Prime Number. —> 16252324
299999977 is Prime Number. —> 16252325
16252325個の素数を検出しました。
0時間37分10秒6889942880002309
構築成功 (合計時間: 37 分 11 秒)

今までのプログラムもこのプログラムも標準出力にすべての素数と何番目か、

それに総数と処理時間を出力していました。

ここで素数を調べるターゲットの数を非常に大きなものにし、標準出力へは

総数と処理時間を表示させるだけのものとしてパフォーマンスの違いを調べてみましょう。

では 2,147,483,640 までの素数を検出させてみます。

まず、前回の並行処理プログラムです。

jp\yucchi\primenumber\PrimeNumber.java

package jp.yucchi.primenumber;

import java.lang.management.ManagementFactory;
import java.util.ArrayList;
import java.util.List;
import java.util.concurrent.*;
import java.util.logging.Level;
import java.util.logging.Logger;

public class PrimeNumber implements Callable<List<Long>> {

    private static final long TARGET_NUMBER = 2_147_483_640L; // 8 の倍数を指定すること(；´Д｀)
    private final long from;
    private final long to;

    public PrimeNumber(final long from, final long to) {
        this.from = from;
        this.to = to;
    }

    public static void main(String[] args) {
        long startTime = System.nanoTime();
        long primeCounter = 0L;
        final int procs = ManagementFactory.getOperatingSystemMXBean().getAvailableProcessors();
        ExecutorService executor = Executors.newFixedThreadPool(procs);
        final long range = TARGET_NUMBER / procs;
        List<Future<List<Long>>> futures = new ArrayList<>();
        for (int i = 0; i < procs; i++) {
            final long from = i * range + 1;
            final long to = (i + 1) * range;
            futures.add(executor.submit(new PrimeNumber(from, to)));
        }
        executor.shutdown();
        List<Long> totalPrimes = new ArrayList<>();
        for (Future<List<Long>> future : futures) {
            try {
                List<Long> primes = future.get();
                totalPrimes.addAll(primes);
            } catch (InterruptedException | ExecutionException ex) {
                Logger.getLogger(PrimeNumber.class.getName()).log(Level.SEVERE, null, ex);
            }
        }
//        for (Long prime : totalPrimes) {
//            primeCounter++;
//            System.out.println(prime + " is Prime Number." + " ---> " + primeCounter);
//        }
//        System.out.println(primeCounter + "個の素数を検出しました。");
        System.out.println(totalPrimes.size());
        long time = System.nanoTime() - startTime;
        System.out.println((int) (time * 1e-9) / 3_600 + "時間"
                + (int) ((time * 1e-9) / 60) % 60 + "分"
                + (int) (time * 1e-9 % 60) + "秒"
                + Double.toString((time * 1e-9 % 60) % 1).substring(2));
    }

    @Override
    public List<Long> call() throws Exception {
        List<Long> primes = new ArrayList<>();
        for (long i = from; i < to + 1L; i++) {
            // 2 より大きな偶数は処理をスキップ
            if ((i & 0b1) == 0 && i > 0b10L) {
                continue;
            }
            long j;
            for (j = (long) Math.sqrt(i); i % j != 0; j--) {
                // i を割り切る j を見つけ出す処理
            }
            // i を割り切れず j が 1 の場合素数と判定、ただし i が 1 の場合は除く        
            if (j == 1L && i != 1L) {
                primes.add(i);
            }
        }
        return primes;
    }
}

package jp.yucchi.primenumber;

import java.lang.management.ManagementFactory;

import java.util.ArrayList;

import java.util.List;

import java.util.concurrent.*;

import java.util.logging.Level;

import java.util.logging.Logger;

public class PrimeNumber implements Callable<List<Long>> {

private static final long TARGET_NUMBER = 2_147_483_640L; // 8 の倍数を指定すること(；´Д｀)

private final long from;

private final long to;

public PrimeNumber(final long from, final long to) {

this.from = from;

this.to = to;

}

public static void main(String[] args) {

long startTime = System.nanoTime();

long primeCounter = 0L;

final int procs = ManagementFactory.getOperatingSystemMXBean().getAvailableProcessors();

ExecutorService executor = Executors.newFixedThreadPool(procs);

final long range = TARGET_NUMBER / procs;

List<Future<List<Long>>> futures = new ArrayList<>();

for (int i = 0; i < procs; i++) {

final long from = i * range + 1;

final long to = (i + 1) * range;

futures.add(executor.submit(new PrimeNumber(from, to)));

}

executor.shutdown();

List<Long> totalPrimes = new ArrayList<>();

for (Future<List<Long>> future : futures) {

try {

List<Long> primes = future.get();

totalPrimes.addAll(primes);

} catch (InterruptedException | ExecutionException ex) {

Logger.getLogger(PrimeNumber.class.getName()).log(Level.SEVERE, null, ex);

}

// for (Long prime : totalPrimes) {

// primeCounter++;

// System.out.println(prime + " is Prime Number." + " ---> " + primeCounter);

// }

// System.out.println(primeCounter + "個の素数を検出しました。");

System.out.println(totalPrimes.size());

long time = System.nanoTime() - startTime;

System.out.println((int) (time * 1e-9) / 3_600 + "時間"

+ (int) ((time * 1e-9) / 60) % 60 + "分"

+ (int) (time * 1e-9 % 60) + "秒"

+ Double.toString((time * 1e-9 % 60) % 1).substring(2));

}

@Override

public List<Long> call() throws Exception {

List<Long> primes = new ArrayList<>();

for (long i = from; i < to + 1L; i++) {

// 2 より大きな偶数は処理をスキップ

if ((i & 0b1) == 0 && i > 0b10L) {

continue;

}

long j;

for (j = (long) Math.sqrt(i); i % j != 0; j--) {

// i を割り切る j を見つけ出す処理

}

// i を割り切れず j が 1 の場合素数と判定、ただし i が 1 の場合は除く

if (j == 1L && i != 1L) {

primes.add(i);

}

return primes;

}

実行結果は次のようにかなりの時間を必要としました。( 15 時間半(；´Д｀) 電気代が・・・）

run:
105097564
15時間26分32秒6862315460020909
構築成功 (合計時間: 926 分 46 秒)

では、最終兵器のエラトステネスの篩ではどうでしょうか？

jp\yucchi\primenumber_eratosthenes\PrimeNumber_Eratosthenes.java

package jp.yucchi.primenumber_eratosthenes;

public class PrimeNumber_Eratosthenes {

    private static final int TARGET_NUMBER = 2_147_483_640;

    public static void main(String[] args) {
        long startTime = System.nanoTime();
        int primeCounter = 0;
        boolean primes[] = new boolean[TARGET_NUMBER];
        for (int i = 2; i < TARGET_NUMBER; i++) {
            // true は素数
            primes[i] = true;
        }
        for (int i = 2; i <= (int) Math.sqrt(TARGET_NUMBER); i++) {
            if (primes[i]) {
                // 素数の倍数を篩にかける
                for (int j = i * 2; 1 < j && j < TARGET_NUMBER; j += i) {
                    primes[j] = false;
                }
            }
        }
        for (int i = 2; i < primes.length; i++) {
            if (primes[i]) {
                primeCounter++;
//                System.out.println(i + " is Prime Number." + " ---> " + primeCounter);
            }
        }
        System.out.println(primeCounter + "個の素数を検出しました。");
        long time = System.nanoTime() - startTime;
        System.out.println((int) (time * 1e-9) / 3_600 + "時間"
                + (int) ((time * 1e-9) / 60) % 60 + "分"
                + (int) (time * 1e-9 % 60) + "秒"
                + Double.toString((time * 1e-9 % 60) % 1).substring(2));
    }
}

package jp.yucchi.primenumber_eratosthenes;

public class PrimeNumber_Eratosthenes {

private static final int TARGET_NUMBER = 2_147_483_640;

public static void main(String[] args) {

long startTime = System.nanoTime();

int primeCounter = 0;

boolean primes[] = new boolean[TARGET_NUMBER];

for (int i = 2; i < TARGET_NUMBER; i++) {

// true は素数

primes[i] = true;

}

for (int i = 2; i <= (int) Math.sqrt(TARGET_NUMBER); i++) {

if (primes[i]) {

// 素数の倍数を篩にかける

for (int j = i * 2; 1 < j && j < TARGET_NUMBER; j += i) {

primes[j] = false;

}

for (int i = 2; i < primes.length; i++) {

if (primes[i]) {

primeCounter++;

// System.out.println(i + " is Prime Number." + " ---> " + primeCounter);

}

System.out.println(primeCounter + "個の素数を検出しました。");

long time = System.nanoTime() - startTime;

System.out.println((int) (time * 1e-9) / 3_600 + "時間"

+ (int) ((time * 1e-9) / 60) % 60 + "分"

+ (int) (time * 1e-9 % 60) + "秒"

+ Double.toString((time * 1e-9 % 60) % 1).substring(2));

}

さて、実行結果はどうなったでしょうか。

run:
105097564個の素数を検出しました。
0時間0分32秒7029516360000017
構築成功 (合計時間: 32 秒)

速っ！＼(◎o◎)／！

この違いは何なんだ！

凄いぜ！　エラトステネスの篩

Hatena タグ: Java

TAGS: Java | 2012年7月5日2:45 PM | Comment : 0

素数を求める vol.2

Java

昨日、素数を求めるプログラムを作ったが 3 億までの素数を求めるのに約 4 時間半かかった。

これが速いのか遅いのかは置いといて、もう少し処理時間の短縮をはかりたい。

最近の PC はマルチコアプロセッサを搭載しているので並列処理させれば処理時間短縮が可能かもしれない。

幸いにも私の PC は 8 コアなので早速試してみました。

ちなみに下記プログラムは、java.util.concurrent パッケージについて調べていた時にあるサイトにあった

サンプルプログラムを参考にさせていただきました。

jp\yucchi\primenumber\PrimeNumber.java

package jp.yucchi.primenumber;

import java.lang.management.ManagementFactory;
import java.util.ArrayList;
import java.util.List;
import java.util.concurrent.*;
import java.util.logging.Level;
import java.util.logging.Logger;

public class PrimeNumber implements Callable<List<Long>> {

    private static final long TARGET_NUMBER = 300_000_000L; // 8 の倍数を指定すること(；´Д｀)
    private final long from;
    private final long to;

    public PrimeNumber(final long from, final long to) {
        this.from = from;
        this.to = to;
    }

    public static void main(String[] args) {
        long startTime = System.nanoTime();
        long primeCounter = 0L;
        final int procs = ManagementFactory.getOperatingSystemMXBean().getAvailableProcessors();
        ExecutorService executor = Executors.newFixedThreadPool(procs);
        final long range = TARGET_NUMBER / procs;
        List<Future<List<Long>>> futures = new ArrayList<>();
        for (int i = 0; i < procs; i++) {
            final long from = i * range + 1;
            final long to = (i + 1) * range;
            futures.add(executor.submit(new PrimeNumber(from, to)));
        }
        executor.shutdown();
        List<Long> totalPrimes = new ArrayList<>();
        for (Future<List<Long>> future : futures) {
            try {
                List<Long> primes = future.get();
                totalPrimes.addAll(primes);
            } catch (InterruptedException | ExecutionException ex) {
                Logger.getLogger(PrimeNumber.class.getName()).log(Level.SEVERE, null, ex);
            }
        }
        for (Long prime : totalPrimes) {
            primeCounter++;
            System.out.println(prime + " is Prime Number." + " ---> " + primeCounter);
        }
        System.out.println(primeCounter + "個の素数を検出しました。");
        long time = System.nanoTime() - startTime;
        System.out.println((int) (time * 1e-9) / 3_600 + "時間"
                + (int) ((time * 1e-9) / 60) % 60 + "分"
                + (int) (time * 1e-9 % 60) + "秒"
                + Double.toString((time * 1e-9 % 60) % 1).substring(2));
    }

    @Override
    public List<Long> call() throws Exception {
        List<Long> primes = new ArrayList<>();
        for (long i = from; i < to + 1L; i++) {
            // 2 より大きな偶数は処理をスキップ
            if ((i & 0b1) == 0 && i > 0b10L) {
                continue;
            }
            long j;
            for (j = (long) Math.sqrt(i); i % j != 0; j--) {
                // i を割り切る j を見つけ出す処理
            }
            // i を割り切れず j が 1 の場合素数と判定、ただし i が 1 の場合は除く        
            if (j == 1L && i != 1L) {
                primes.add(i);
            }
        }
        return primes;
    }
}

package jp.yucchi.primenumber;

import java.lang.management.ManagementFactory;

import java.util.ArrayList;

import java.util.List;

import java.util.concurrent.*;

import java.util.logging.Level;

import java.util.logging.Logger;

public class PrimeNumber implements Callable<List<Long>> {

private static final long TARGET_NUMBER = 300_000_000L; // 8 の倍数を指定すること(；´Д｀)

private final long from;

private final long to;

public PrimeNumber(final long from, final long to) {

this.from = from;

this.to = to;

}

public static void main(String[] args) {

long startTime = System.nanoTime();

long primeCounter = 0L;

final int procs = ManagementFactory.getOperatingSystemMXBean().getAvailableProcessors();

ExecutorService executor = Executors.newFixedThreadPool(procs);

final long range = TARGET_NUMBER / procs;

List<Future<List<Long>>> futures = new ArrayList<>();

for (int i = 0; i < procs; i++) {

final long from = i * range + 1;

final long to = (i + 1) * range;

futures.add(executor.submit(new PrimeNumber(from, to)));

}

executor.shutdown();

List<Long> totalPrimes = new ArrayList<>();

for (Future<List<Long>> future : futures) {

try {

List<Long> primes = future.get();

totalPrimes.addAll(primes);

} catch (InterruptedException | ExecutionException ex) {

Logger.getLogger(PrimeNumber.class.getName()).log(Level.SEVERE, null, ex);

}

for (Long prime : totalPrimes) {

primeCounter++;

System.out.println(prime + " is Prime Number." + " ---> " + primeCounter);

}

System.out.println(primeCounter + "個の素数を検出しました。");

long time = System.nanoTime() - startTime;

System.out.println((int) (time * 1e-9) / 3_600 + "時間"

+ (int) ((time * 1e-9) / 60) % 60 + "分"

+ (int) (time * 1e-9 % 60) + "秒"

+ Double.toString((time * 1e-9 % 60) % 1).substring(2));

}

@Override

public List<Long> call() throws Exception {

List<Long> primes = new ArrayList<>();

for (long i = from; i < to + 1L; i++) {

// 2 より大きな偶数は処理をスキップ

if ((i & 0b1) == 0 && i > 0b10L) {

continue;

}

long j;

for (j = (long) Math.sqrt(i); i % j != 0; j--) {

// i を割り切る j を見つけ出す処理

}

// i を割り切れず j が 1 の場合素数と判定、ただし i が 1 の場合は除く

if (j == 1L && i != 1L) {

primes.add(i);

}

return primes;

}

このプログラムの実行結果は次のようになった。

2 is Prime Number. —> 1
3 is Prime Number. —> 2
5 is Prime Number. —> 3
7 is Prime Number. —> 4
11 is Prime Number. —> 5
13 is Prime Number. —> 6
17 is Prime Number. —> 7
19 is Prime Number. —> 8
23 is Prime Number. —> 9
29 is Prime Number. —> 10

　　　　略

299999801 is Prime Number. —> 16252317
299999807 is Prime Number. —> 16252318
299999813 is Prime Number. —> 16252319
299999827 is Prime Number. —> 16252320
299999897 is Prime Number. —> 16252321
299999923 is Prime Number. —> 16252322
299999939 is Prime Number. —> 16252323
299999957 is Prime Number. —> 16252324
299999977 is Prime Number. —> 16252325
16252325個の素数を検出しました。
1時間26分23秒42106727300051716

なんと 3 時間も処理時間が短縮できました。(^_^)v

それでも 1 時間半近くかかります。

こんなものなのかなぁ・・・？

素数を求めるアルゴリズムにエラトステネスの篩ってのがあります。

それも試してみましょう。

それでは

おっとそろそろ時間が・・・

~~続きは Web で！~~

つづきはまた今度ね♪

Hatena タグ: Java

TAGS: Java | 2012年6月25日8:15 AM | Comment : 0

« 古い記事新しい記事 »

ゆっちのBlog

Solaris 11 インストール vol.2

Solaris 11 インストール

素数を求める vol.4 （おまけ）

素数を求める vol.3

素数を求める vol.2

Recent Comments

Java

NetBeans

カテゴリー

アーカイブ

RSS FEED

ねこび～ん

メタ情報

ゆっちのカレンダー

2012年1月
月	火	水	木	金	土	日
				5月 »
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30	31

ゆっちのBlog

Solaris 11 インストール vol.2

Solaris 11 インストール

素数を求める vol.4 （おまけ）

素数を求める vol.3

素数を求める vol.2

Popular post ranking

Recent Comments

Java

NetBeans

カテゴリー

アーカイブ

RSS FEED

ねこび～ん

メタ情報

ゆっちのカレンダー