ゆっちのBlog

2013年 1月

実行可能JARファイルが Java 7 u11 で動くようになっていた

Java

実行可能JARファイルが Java 7 になってから動かなくなってがっかりしていたが Windows 8 Pro , Java 7 u11 で動くことを確認！

いつから動くようになったのかは不明です。

また、Windows 7 での確認はまだしていません。

これで過去に作った自分専用の Java アプリが使えます。（＾＾）

そう言えばこの件をネットで調べていたとき同じように Java 7 で動かなくなって弱ってる人を発見しました。

早速教えてあげようと思ったがどこのサイトだったか記憶にない（＾＾；

Hatena タグ: Java

TAGS: Java | 2013年1月30日5:10 PM | Comment : 0

Men in Black 3

Movie

おもしろかった（＾＾）

いつもながらのコンビの良さに安心できる。

しかし今回の作品は何故ＪがＫにスカウトされる運命にあったか

ＫとＪの過去に迫る作品となっていた。

ここでそれを語るとネタバレになるからやめておこう。

そうそう、Ｋは日本の缶コーヒーＢＯＳＳのコマーシャルやってるのに

コーヒーの味を「動物の死骸みたいな味だ」といっているのは笑えた。

「当たり前よ、今朝挽いた（轢いた）ばかり」といった返しでなりったってるけどちょっときついジョークですね。

細かい笑いの仕掛けがいたるところにあるので楽しめます。

大人が楽しめるようなラブストーリーではないが子供心を忘れていない大人に是非ご覧になっていただきたい。

あれっ？

チョコレートミルクが無性に飲みたくなってきたのは何故だ！

Hatena タグ: Movie

TAGS: Movie | 2013年1月19日8:24 PM | Comment : 0

るろうに剣心

Movie

私は時代劇はあまり好きではないがチャンバラは好きだ。

チャンバラという言い方は不適切だな。

格好いい派手な殺陣が好きだ。

最近殺陣が話題になるような時代劇は無かったと思う。

この映画で評論家が殺陣が斬新で素晴らしいと褒めていた。

出演者達もそうそうたるメンバーなのに演じ方とか褒めずに殺陣を褒めていた。

そこでレンタル開始されたので借りて見たところ素晴らしかった。

これは監督のこだわりだろう。

いい意味でこの殺陣だけでもこの映画は成立するといっても過言ではないだろう。

ただし、本格的時代劇ファンにとってはただのＢ級映画かもしれない。

もともと少年ジャンプに連載されていた漫画が原作なので大人向けのストーリーではない。

それが故に安心して楽しめる。

私は原作を読んでないので映画のストーリーを評価できないがそれでも楽しめた。

続編が作られたら必ず見てみたい作品である。

Hatena タグ: Movie

TAGS: Movie | 2013年1月9日7:23 PM | Comment : 0

Nクイーン問題 nQueens Problem

Java

Java で Nクイーン問題　nQueens Problem をプログラミングしてみました。

まず Nクイーン問題とは何か？

ネットでググってみると８クイーン問題ってのがよくとりあげられてます。

Nクイーン問題とはそれを一般化したようです。

では８クイーン問題から調べていきましょう。

８クイーン問題では、王妃（クイーン）８個が用意されています。

チェス盤のサイズは王妃（クイーン）と同じ数とします。

８クイーンでは縦、横８マスです。

そのチェス盤に全ての王妃（クイーン）を配置します。

ただし、それぞれの王妃（クイーン）の利き筋には配置できません。（縦、横、斜めの４ライン）

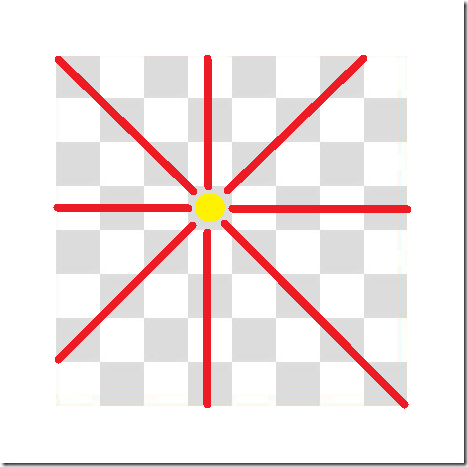
以上の条件を全て満たす王妃（クイーン）の配置パターン及び総数を求めるものです。

それではどうやって解を導き出したらいいのか考えてみることにします。

８個の王妃（クイーン）を全ての組み合わせに配置して上記の条件をクリアするかを確認すればいいだけのことですね。

しかし、その方法だと 8 X 8 = 64 マスあるから

64 X 63 X 62 X 61 X 60 X 59 X 58 X 57 = 178,462,987,637,760 通りもあることになります。

ちょっと多いですね。

王妃（クイーン）の数が大きくなった時のことを考えたら厳しいです。

しかし、全ての組み合わせを調べる必要はなさそうです。

何故なら、同じ列、行に王妃は配置できないからです。

縦、横の利き筋の条件を考慮した結果、各列、行には王妃（クイーン）は 1 個だけしか配置できない！

よって、 8! = 40,320 通りまで激減させることができる。

あと斜めの利き筋２つを利用すれば計算処理はもっと少なくなるだろう。

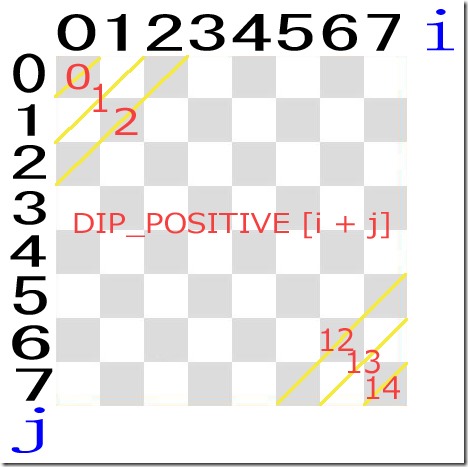
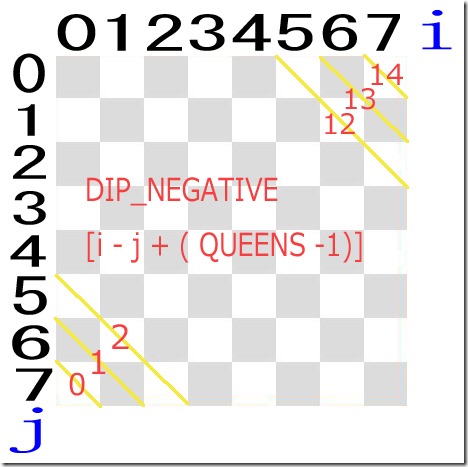
以上のことを考慮した上で次のようなプログラムを作ればいいかもしれない。

private static void trySet(int i) {

for (王妃の数だけループ) {

if (利き筋から外れていれば) {

王妃 i 列 j 行に配置

if (i == (王妃８個配置できたら) {

トータルパターン数をカウントアップ

盤面を表示

}else {

王妃の利き筋（行、斜め）をセット

次の列を配置（再帰 trySet(i + 1)）

王妃の利き筋（行、斜め）を解除

                    }
             }
     }
}

ってことで作ってみました。

ただ、デバッガでプログラムの流れを追うために王妃（クイーン）の数は 4 としました。

もちろん、王妃（クイーン）の数は一般化できるようにしてあります。

nqueensproblem.NQueensProblem.java

package nqueensproblem;

/**
 *
 * @author Yucchi
 */
public class NQueensProblem {

    // 王妃数
    private static final int QUEENS = 4;
    // 王妃の配置位置 
    private static final int [] VERTICAL = new int [QUEENS];
    // 行に王妃が配置されてるかチェック用  
    private static final boolean [] HORIZONTAL = new boolean [QUEENS]; 
    // 右４５度斜めラインに王妃が配置されているかチェック用
    private static final boolean [] DIP_POSITIVE = new boolean [QUEENS * 2 -1]; 
    // 左４５度斜めラインに王妃が配置されているかチェック用
    private static final boolean [] DIP_NEGATIVE = new boolean [QUEENS * 2 - 1];
    // 安全 
    private static final boolean SAFE = false;
    // 危険 
    private static final boolean OUT = true;
    // トータルパターン数 
    private static int counter; 

    public static void main(String[] args) {
        trySet(0);
        if(counter < 1){
            System.out.println("配置不可能でした。");
        }else{
            System.out.println(counter + " パターン配置可能でした。");
        }
    }
    
    // 全ての可能な王妃の配置位置を取得、そしてトータルパターン数も取得する。
    private static void trySet(int i) {
        for (int j = 0; j < QUEENS; j++) {
            // 行 ( j )、／右４５度斜めライン ( i + j )、＼左４５度斜めライン (i - j + ( QUEENS -1 )) 配置チェック
         if (HORIZONTAL [j] == SAFE && DIP_POSITIVE [i + j] == SAFE && DIP_NEGATIVE [i - j + ( QUEENS -1)] == SAFE) { 
            VERTICAL [i] = j; // 王妃 i 列 j 行に配置
            if (i == ( QUEENS -1)) { // 王妃の配置完了
                 counter++; // トータルパターン数カウンター
                 printBoard(); // 盤面を表示
             }else {
                // 王妃の利き筋（行、斜め）をセット
               HORIZONTAL [j] = DIP_POSITIVE [i + j] = DIP_NEGATIVE [i - j + ( QUEENS -1)] = OUT;
               // 次の列を配置
               trySet(i + 1);
               // 王妃の利き筋（行、斜め）を解除
               HORIZONTAL [j] = DIP_POSITIVE [i + j] = DIP_NEGATIVE [i - j + ( QUEENS -1)] = SAFE;
            }
         }
      }
    }

    // 全ての可能な王位配置位置を出力　●が王妃が置かれた場所である。
    private static void printBoard() {
        System.out.println("第 " + counter + " パターン"); 
        for (int i = 0; i < QUEENS; i++) {
         for (int j = 0; j < QUEENS; j++) {
                System.out.printf("%s", j == VERTICAL [i] ? "● " : "□ ");
            }
         System.out.println();
      }
      System.out.println();

    }
}

package nqueensproblem;

/**

* @author Yucchi

public class NQueensProblem {

// 王妃数

private static final int QUEENS = 4;

// 王妃の配置位置

private static final int [] VERTICAL = new int [QUEENS];

// 行に王妃が配置されてるかチェック用

private static final boolean [] HORIZONTAL = new boolean [QUEENS];

// 右４５度斜めラインに王妃が配置されているかチェック用

private static final boolean [] DIP_POSITIVE = new boolean [QUEENS * 2 -1];

// 左４５度斜めラインに王妃が配置されているかチェック用

private static final boolean [] DIP_NEGATIVE = new boolean [QUEENS * 2 - 1];

// 安全

private static final boolean SAFE = false;

// 危険

private static final boolean OUT = true;

// トータルパターン数

private static int counter;

public static void main(String[] args) {

trySet(0);

if(counter < 1){

System.out.println("配置不可能でした。");

}else{

System.out.println(counter + " パターン配置可能でした。");

}

// 全ての可能な王妃の配置位置を取得、そしてトータルパターン数も取得する。

private static void trySet(int i) {

for (int j = 0; j < QUEENS; j++) {

// 行 ( j )、／右４５度斜めライン ( i + j )、＼左４５度斜めライン (i - j + ( QUEENS -1 )) 配置チェック

if (HORIZONTAL [j] == SAFE && DIP_POSITIVE [i + j] == SAFE && DIP_NEGATIVE [i - j + ( QUEENS -1)] == SAFE) {

VERTICAL [i] = j; // 王妃 i 列 j 行に配置

if (i == ( QUEENS -1)) { // 王妃の配置完了

counter++; // トータルパターン数カウンター

printBoard(); // 盤面を表示

}else {

// 王妃の利き筋（行、斜め）をセット

HORIZONTAL [j] = DIP_POSITIVE [i + j] = DIP_NEGATIVE [i - j + ( QUEENS -1)] = OUT;

// 次の列を配置

trySet(i + 1);

// 王妃の利き筋（行、斜め）を解除

HORIZONTAL [j] = DIP_POSITIVE [i + j] = DIP_NEGATIVE [i - j + ( QUEENS -1)] = SAFE;

}

// 全ての可能な王位配置位置を出力　●が王妃が置かれた場所である。

private static void printBoard() {

System.out.println("第 " + counter + " パターン");

for (int i = 0; i < QUEENS; i++) {

for (int j = 0; j < QUEENS; j++) {

System.out.printf("%s", j == VERTICAL [i] ? "● " : "□ ");

}

System.out.println();

}

System.out.println();

}

さて、理屈やコードだけでは解りにくいかもしれないのでこのプログラムの流れをデバッグ実行して確認してみます。

デバッグウィンドウやウォッチポイントの変数の値を確認しながらごらんくださいませ。

プログラムの流れを見ていると人間の思考原理に非常に良く似ていますね。

とりあえず順番に試してみる。

条件を考慮して無駄なことはせず作業量を減らす。

途中で駄目だと判断できたら戻って次のパターンからやり直す。

それの繰り返しで処理を完了する。

こういったアルゴリズムはバックトラック法って言われているようです。

深さ優先探索アルゴリズムですね。

試行錯誤的に解を探し出すタイプの問題に有効です。

つまり、基本的に全ての選択肢を試してみるしか無い場合なんかには有効のようです。

いつ頃、誰が、どのような理由でこういったアルゴリズムを考えたのか？

考えた人を心から尊敬します。

ちなみに８王妃問題としてプログラムを実行したい場合は上記プログラムの 9 行目の

private static final int QUEENS = 4; // 王妃数

王妃数を 8 に変更してください。

任意の王妃数をこれによって設定できますがあまり王妃数を大きくすると計算量が指数関数的に増加するでしょうからほどほどに(^_^;

再帰アルゴリズムについてはこちらで簡単な覚え書きを残してあります。

再帰アルゴリズム　その１

再帰アルゴリズム　その２

ユークリッドの互除法 Euclidean Algorithm

ハノイの塔 Tower of Hanoi

Hatena タグ: Java

TAGS: Java | 2013年1月5日6:58 AM | Comment : 0

ハノイの塔 Tower of Hanoi

Java

Java でハノイの塔をプログラミングしてみました。

再帰アルゴリズムでググるとほとんどの言語でサンプルがあります。

しかし、再帰アルゴリズムは理屈では理解できても実際に使おうとすると難しいものです。

そこで NetBeans を使って再帰アルゴリズムの仕組みをみていこうと思います。

まず、ハノイの塔についておさらいしておきましょう。

Wikipedia によると、ハノイの塔は、フランスの数学者エドゥアール・リュカが1883年に発売したゲーム『ハノイの塔』がルーツである。

その内容は下記のようになっている。

インドのガンジス河の畔のヴァラナシ（ベナレス）に、世界の中心を表すという巨大な寺院がある。

そこには青銅の板の上に、長さ1キュビット、太さが蜂の体ほどの3本のダイヤモンドの針が立てられている。

そのうちの1本には、天地創造のときに神が64枚の純金の円盤を大きい円盤から順に重ねて置いた。

これが「ブラフマーの塔」である。司祭たちはそこで、昼夜を通して円盤を別の柱に移し替えている（移し替えのルールの説明は省略）。

そして、全ての円盤の移し替えが終わったときに、世界は崩壊し終焉を迎える。

n 枚の円盤すべてを移動させるには最低 2^n-1 回(2のｎ乗 – 1 回)の手数がかかります。

なんか恐ろしいですね。

それにハノイの塔じゃなくてブラフマーの塔になってます。（なんでだろう？ )

さて。肝心の移し替えのルールをザックリと確認しましょう。

移し替えの際、円盤は一回に一枚しか移し替えできない。

小さな円盤の上に大きな円盤を重ね置くことはできない。

実にシンプルなルールですね。

しかし、シンプルだからといって侮れません。

考え方としては円盤の枚数を n 枚とします。

そして円盤が重ね置いてあるダイヤの針は左( LEFT )とします。

移し替え先のダイヤの針は右( RIGHT )、そして移し替え作業用のダイヤの針を中央( CENTER )とします。

まず、n -1 枚の円盤を中央のダイヤの針に移し替えます。

そして、右のダイヤの針に左のダイヤの針に残っている一番大きな円盤( n 枚目の円盤 )を移し替えます。

次に中央のダイヤの針に移し替えられた n-1 枚の円盤を左のダイヤの針に移し替えます。

言葉よりプログラムの流れで確認したほうが理解し易いかもしれませんね。

上記の考え方を再帰アルゴリズムを利用して組んだコードがこれです。

素人が作ったプログラムなので読みにくいとは思いますがじっくりプログラムの流れを確認してください。

yucchi.jp.hanoi.Hanoi.java

package yucchi.jp.hanoi;

/**
 *
 * @author Yucchi
 */
public class Hanoi {

    private static int count;
    private static int TARGET_NUMBER = 3;

    // ハノイの塔
    // n : 移動させる円盤の枚数
    // from : 移動元の塔
    // work : 作業用の塔 ---> 一番下の円盤以外の一時的な置き場所
    // dest : 移動先の塔
    private static void hanoi(int n, String from, String work, String dest) {
        if (n > 0) {
            // n - 1 番目の輪を LEFT から CENTER に移動させる。
            hanoi(n - 1, from, dest, work);
            // 上の hanoi(n - 1, from, dest, work)を実行完了後に
            // n 番目の円盤を移動させる。
            System.out.println(++count + " ： " + n + "番目の円盤を" + from + "から" + dest + "へ移動させる。");
            // 上の hanoi(n - 1, from, dest, work) メソッドで
            // 一番下以外の棒がfromからworkに移っているので、
            // 今度は work を from にして、空いた from を work にして移動させる。
            // n - 1 番目の輪を CENTER から LEFT に移動させる。
            hanoi(n - 1, work, from, dest);
        }
    }

    public static void main(String[] args) {
        System.out.println(TARGET_NUMBER + "枚のハノイの塔　開始");
        // ダイアでできた LEFT 塔にある TARGET_NUMBER 枚の純金の円盤をダイアでできた RIGHT 塔に移動させる。
        hanoi(TARGET_NUMBER, "LEFT", "CENTER", "RIGHT");
        System.out.println(TARGET_NUMBER + "枚のハノイの塔　終了");
    }
}

package yucchi.jp.hanoi;

/**

* @author Yucchi

public class Hanoi {

private static int count;

private static int TARGET_NUMBER = 3;

// ハノイの塔

// n : 移動させる円盤の枚数

// from : 移動元の塔

// work : 作業用の塔 ---> 一番下の円盤以外の一時的な置き場所

// dest : 移動先の塔

private static void hanoi(int n, String from, String work, String dest) {

if (n > 0) {

// n - 1 番目の輪を LEFT から CENTER に移動させる。

hanoi(n - 1, from, dest, work);

// 上の hanoi(n - 1, from, dest, work)を実行完了後に

// n 番目の円盤を移動させる。

System.out.println(++count + " ： " + n + "番目の円盤を" + from + "から" + dest + "へ移動させる。");

// 上の hanoi(n - 1, from, dest, work) メソッドで

// 一番下以外の棒がfromからworkに移っているので、

// 今度は work を from にして、空いた from を work にして移動させる。

// n - 1 番目の輪を CENTER から LEFT に移動させる。

hanoi(n - 1, work, from, dest);

}

public static void main(String[] args) {

System.out.println(TARGET_NUMBER + "枚のハノイの塔　開始");

// ダイアでできた LEFT 塔にある TARGET_NUMBER 枚の純金の円盤をダイアでできた RIGHT 塔に移動させる。

hanoi(TARGET_NUMBER, "LEFT", "CENTER", "RIGHT");

System.out.println(TARGET_NUMBER + "枚のハノイの塔　終了");

}

どうでしょうか？

理解できましたでしょうか？

考え方は非常にシンプルだけどけっこう流れは追っていくと複雑に感じますね。

いちおう参考までにこれも貼っておきます。

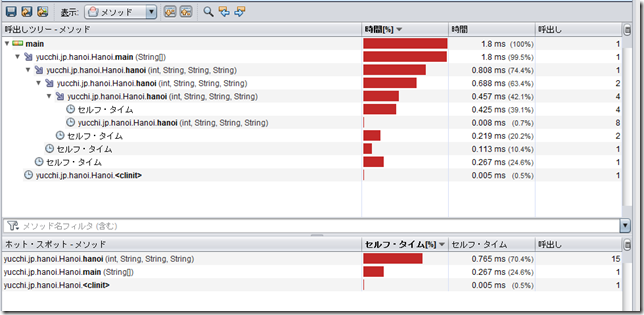
hanoi メソッドが再帰的に実行されているのが確認できます。

これで再帰アルゴリズムで複雑な繰り返し処理を記述できるようになったとはとても思えないけど

ちょっとは再帰アルゴリズムの使いどころを理解したつもりになりました。

たぶん、すぐに忘れてしまうだろうけどまた挑戦してみたらいいだけのことだし。

気楽に楽しんでいこう！ (*^o^*)

再帰アルゴリズムについてはこちらで簡単な覚え書きを残してあります。

再帰アルゴリズム　その１

再帰アルゴリズム　その２

ユークリッドの互除法 Euclidean Algorithm

Hatena タグ: Java

TAGS: Java | 2013年1月4日5:03 AM | Comment : 1

« 古い記事

月	火	水	木	金	土	日
« 12月				2月 »
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30	31

実行可能JARファイルが Java 7 u11 で動くようになっていた

Men in Black 3

るろうに剣心

Nクイーン問題 nQueens Problem

ハノイの塔 Tower of Hanoi

Recent Comments

Java

NetBeans

カテゴリー

アーカイブ

RSS FEED

ねこび～ん

メタ情報

ゆっちのカレンダー

ゆっちのBlog

実行可能JARファイルが Java 7 u11 で動くようになっていた

Men in Black 3

るろうに剣心

Nクイーン問題 nQueens Problem

ハノイの塔 Tower of Hanoi

Popular post ranking

Recent Comments

Java

NetBeans

カテゴリー

アーカイブ

RSS FEED

ねこび～ん

メタ情報

ゆっちのカレンダー