Nクイーン問題 nQueens Problem
Java で Nクイーン問題 nQueens Problem をプログラミングしてみました。
まず Nクイーン問題とは何か?
ネットでググってみると8クイーン問題ってのがよくとりあげられてます。
Nクイーン問題とはそれを一般化したようです。
では8クイーン問題から調べていきましょう。
8クイーン問題では、王妃(クイーン)8個が用意されています。
チェス盤のサイズは王妃(クイーン)と同じ数とします。
8クイーンでは縦、横8マスです。
そのチェス盤に全ての王妃(クイーン)を配置します。
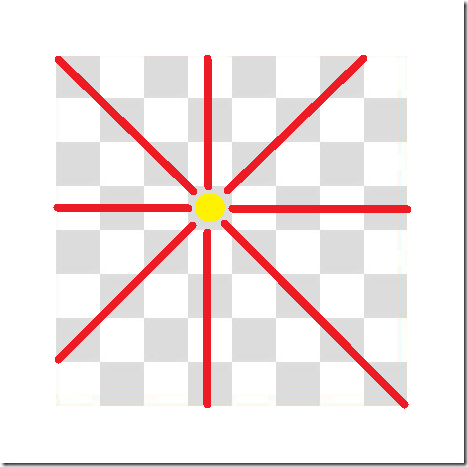
ただし、それぞれの王妃(クイーン)の利き筋には配置できません。(縦、横、斜めの4ライン)
以上の条件を全て満たす王妃(クイーン)の配置パターン及び総数を求めるものです。
それではどうやって解を導き出したらいいのか考えてみることにします。
8個の王妃(クイーン)を全ての組み合わせに配置して上記の条件をクリアするかを確認すればいいだけのことですね。
しかし、その方法だと 8 X 8 = 64 マスあるから
64 X 63 X 62 X 61 X 60 X 59 X 58 X 57 = 178,462,987,637,760 通りもあることになります。
ちょっと多いですね。
王妃(クイーン)の数が大きくなった時のことを考えたら厳しいです。
しかし、全ての組み合わせを調べる必要はなさそうです。
何故なら、同じ列、行に王妃は配置できないからです。
縦、横の利き筋の条件を考慮した結果、各列、行には王妃(クイーン)は 1 個だけしか配置できない!
よって、 8! = 40,320 通りまで激減させることができる。
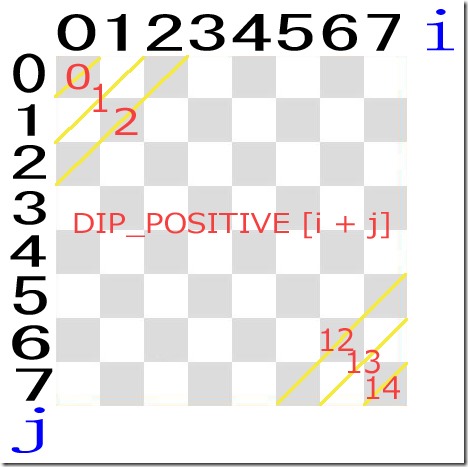
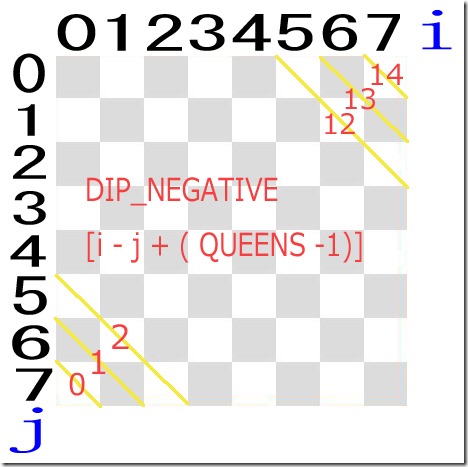
あと斜めの利き筋2つを利用すれば計算処理はもっと少なくなるだろう。
以上のことを考慮した上で次のようなプログラムを作ればいいかもしれない。
private static void trySet(int i) {
for (王妃の数だけループ) {
if (利き筋から外れていれば) {
王妃 i 列 j 行に配置
if (i == (王妃8個配置できたら) {
トータルパターン数をカウントアップ
盤面を表示
}else {
王妃の利き筋(行、斜め)をセット
次の列を配置(再帰 trySet(i + 1))
王妃の利き筋(行、斜め)を解除
}
}
}
}
ってことで作ってみました。
ただ、デバッガでプログラムの流れを追うために王妃(クイーン)の数は 4 としました。
もちろん、王妃(クイーン)の数は一般化できるようにしてあります。
| nqueensproblem.NQueensProblem.java |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
package nqueensproblem; /** * * @author Yucchi */ public class NQueensProblem { // 王妃数 private static final int QUEENS = 4; // 王妃の配置位置 private static final int [] VERTICAL = new int [QUEENS]; // 行に王妃が配置されてるかチェック用 private static final boolean [] HORIZONTAL = new boolean [QUEENS]; // 右45度斜めラインに王妃が配置されているかチェック用 private static final boolean [] DIP_POSITIVE = new boolean [QUEENS * 2 -1]; // 左45度斜めラインに王妃が配置されているかチェック用 private static final boolean [] DIP_NEGATIVE = new boolean [QUEENS * 2 - 1]; // 安全 private static final boolean SAFE = false; // 危険 private static final boolean OUT = true; // トータルパターン数 private static int counter; public static void main(String[] args) { trySet(0); if(counter < 1){ System.out.println("配置不可能でした。"); }else{ System.out.println(counter + " パターン配置可能でした。"); } } // 全ての可能な王妃の配置位置を取得、そしてトータルパターン数も取得する。 private static void trySet(int i) { for (int j = 0; j < QUEENS; j++) { // 行 ( j )、/右45度斜めライン ( i + j )、\左45度斜めライン (i - j + ( QUEENS -1 )) 配置チェック if (HORIZONTAL [j] == SAFE && DIP_POSITIVE [i + j] == SAFE && DIP_NEGATIVE [i - j + ( QUEENS -1)] == SAFE) { VERTICAL [i] = j; // 王妃 i 列 j 行に配置 if (i == ( QUEENS -1)) { // 王妃の配置完了 counter++; // トータルパターン数カウンター printBoard(); // 盤面を表示 }else { // 王妃の利き筋(行、斜め)をセット HORIZONTAL [j] = DIP_POSITIVE [i + j] = DIP_NEGATIVE [i - j + ( QUEENS -1)] = OUT; // 次の列を配置 trySet(i + 1); // 王妃の利き筋(行、斜め)を解除 HORIZONTAL [j] = DIP_POSITIVE [i + j] = DIP_NEGATIVE [i - j + ( QUEENS -1)] = SAFE; } } } } // 全ての可能な王位配置位置を出力 ●が王妃が置かれた場所である。 private static void printBoard() { System.out.println("第 " + counter + " パターン"); for (int i = 0; i < QUEENS; i++) { for (int j = 0; j < QUEENS; j++) { System.out.printf("%s", j == VERTICAL [i] ? "● " : "□ "); } System.out.println(); } System.out.println(); } } |
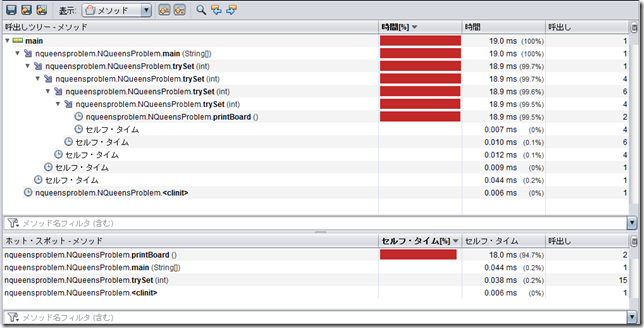
さて、理屈やコードだけでは解りにくいかもしれないのでこのプログラムの流れをデバッグ実行して確認してみます。
デバッグウィンドウやウォッチポイントの変数の値を確認しながらごらんくださいませ。
プログラムの流れを見ていると人間の思考原理に非常に良く似ていますね。
とりあえず順番に試してみる。
条件を考慮して無駄なことはせず作業量を減らす。
途中で駄目だと判断できたら戻って次のパターンからやり直す。
それの繰り返しで処理を完了する。
こういったアルゴリズムはバックトラック法って言われているようです。
深さ優先探索アルゴリズムですね。
試行錯誤的に解を探し出すタイプの問題に有効です。
つまり、基本的に全ての選択肢を試してみるしか無い場合なんかには有効のようです。
いつ頃、誰が、どのような理由でこういったアルゴリズムを考えたのか?
考えた人を心から尊敬します。
ちなみに 8王妃問題としてプログラムを実行したい場合は上記プログラムの 9 行目の
private static final int QUEENS = 4; // 王妃数
王妃数を 8 に変更してください。
任意の王妃数をこれによって設定できますがあまり王妃数を大きくすると計算量が指数関数的に増加するでしょうからほどほどに(^_^;
再帰アルゴリズムについてはこちらで簡単な覚え書きを残してあります。
ユークリッドの互除法 Euclidean Algorithm
TAGS: Java | 2013年1月5日6:58 AM

Trackback URL