2013
Java
Java でハノイの塔をプログラミングしてみました。
再帰アルゴリズムでググるとほとんどの言語でサンプルがあります。
しかし、再帰アルゴリズムは理屈では理解できても実際に使おうとすると難しいものです。
そこで NetBeans を使って再帰アルゴリズムの仕組みをみていこうと思います。
まず、ハノイの塔についておさらいしておきましょう。
Wikipedia によると、ハノイの塔は、フランスの数学者エドゥアール・リュカが1883年に発売したゲーム『ハノイの塔』がルーツである。
その内容は下記のようになっている。
インドのガンジス河の畔のヴァラナシ(ベナレス)に、世界の中心を表すという巨大な寺院がある。
そこには青銅の板の上に、長さ1キュビット、太さが蜂の体ほどの3本のダイヤモンドの針が立てられている。
そのうちの1本には、天地創造のときに神が64枚の純金の円盤を大きい円盤から順に重ねて置いた。
これが「ブラフマーの塔」である。司祭たちはそこで、昼夜を通して円盤を別の柱に移し替えている(移し替えのルールの説明は省略)。
そして、全ての円盤の移し替えが終わったときに、世界は崩壊し終焉を迎える。
n 枚の円盤すべてを移動させるには最低 2^n-1 回(2のn乗 – 1 回)の手数がかかります。
なんか恐ろしいですね。
それにハノイの塔じゃなくてブラフマーの塔になってます。( なんでだろう? )
さて。肝心の移し替えのルールをザックリと確認しましょう。
移し替えの際、円盤は一回に一枚しか移し替えできない。
小さな円盤の上に大きな円盤を重ね置くことはできない。
実にシンプルなルールですね。
しかし、シンプルだからといって侮れません。
考え方としては円盤の枚数を n 枚とします。
そして円盤が重ね置いてあるダイヤの針は左( LEFT )とします。
移し替え先のダイヤの針は右( RIGHT )、そして移し替え作業用のダイヤの針を中央( CENTER )とします。
まず、n -1 枚の円盤を中央のダイヤの針に移し替えます。
そして、右のダイヤの針に左のダイヤの針に残っている一番大きな円盤( n 枚目の円盤 )を移し替えます。
次に中央のダイヤの針に移し替えられた n-1 枚の円盤を左のダイヤの針に移し替えます。
言葉よりプログラムの流れで確認したほうが理解し易いかもしれませんね。
上記の考え方を再帰アルゴリズムを利用して組んだコードがこれです。
素人が作ったプログラムなので読みにくいとは思いますがじっくりプログラムの流れを確認してください。
| yucchi.jp.hanoi.Hanoi.java |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
package yucchi.jp.hanoi; /** * * @author Yucchi */ public class Hanoi { private static int count; private static int TARGET_NUMBER = 3; // ハノイの塔 // n : 移動させる円盤の枚数 // from : 移動元の塔 // work : 作業用の塔 ---> 一番下の円盤以外の一時的な置き場所 // dest : 移動先の塔 private static void hanoi(int n, String from, String work, String dest) { if (n > 0) { // n - 1 番目の輪を LEFT から CENTER に移動させる。 hanoi(n - 1, from, dest, work); // 上の hanoi(n - 1, from, dest, work)を実行完了後に // n 番目の円盤を移動させる。 System.out.println(++count + " : " + n + "番目の円盤を" + from + "から" + dest + "へ移動させる。"); // 上の hanoi(n - 1, from, dest, work) メソッドで // 一番下以外の棒がfromからworkに移っているので、 // 今度は work を from にして、空いた from を work にして移動させる。 // n - 1 番目の輪を CENTER から LEFT に移動させる。 hanoi(n - 1, work, from, dest); } } public static void main(String[] args) { System.out.println(TARGET_NUMBER + "枚のハノイの塔 開始"); // ダイアでできた LEFT 塔にある TARGET_NUMBER 枚の純金の円盤をダイアでできた RIGHT 塔に移動させる。 hanoi(TARGET_NUMBER, "LEFT", "CENTER", "RIGHT"); System.out.println(TARGET_NUMBER + "枚のハノイの塔 終了"); } } |
どうでしょうか?
理解できましたでしょうか?
考え方は非常にシンプルだけどけっこう流れは追っていくと複雑に感じますね。
いちおう参考までにこれも貼っておきます。
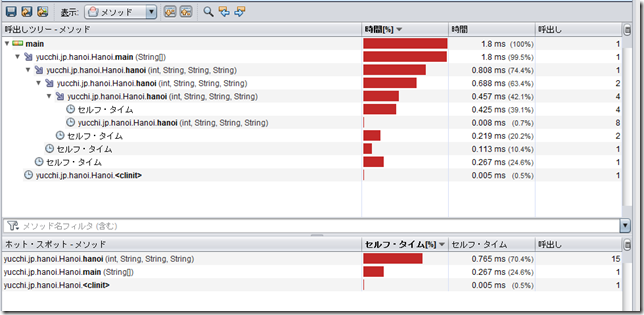
hanoi メソッドが再帰的に実行されているのが確認できます。
これで再帰アルゴリズムで複雑な繰り返し処理を記述できるようになったとはとても思えないけど
ちょっとは再帰アルゴリズムの使いどころを理解したつもりになりました。
たぶん、すぐに忘れてしまうだろうけどまた挑戦してみたらいいだけのことだし。
気楽に楽しんでいこう! (*^o^*)

再帰アルゴリズムについてはこちらで簡単な覚え書きを残してあります。
再帰アルゴリズム その1
再帰アルゴリズム その2
ユークリッドの互除法 Euclidean Algorithm
TAGS: Java |
2013年1月4日5:03 AM |
Java
Java でユークリッドの互除法 Euclidean Algorithm をプログラミングしてみました。
再帰アルゴリズムを使ってます。
再帰アルゴリズムについてはこちらで簡単な覚え書きを残してあります。
再帰アルゴリズム その1
再帰アルゴリズム その2
ユークリッドの互除法とはいったいどんな仕組みなのか調べてみました。
ある二つの自然数の最大公約数を求めるのに非常に優れた方法らしいです。
名前に互除法とあるとおり互いに割り算を行って解を導き出す方法です。
簡単に説明すると自然数 r1 と r 2 ( r1 >= r2 ) の最大公約数を求めるとき ( 注意 : r の後の数字と n は小さい数字だと思ってください。)
r1 / r2 の余り r3 を求める。
次に r2 / r3 の余り r4 を・・・
これを rn が 0 になるまで繰り返す。
この時、 r(n-1) が最大公約数となる。
実にシンプルです。
数学的証明はここでは割愛させていただきます。
これを Java プログラムにするには再帰アルゴリズムを使えば簡単にできそうですね。
さっそく作ってみましょう。
| euclidean_algorithm.Euclidean_Algorithm.java |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
package euclidean_algorithm; /** * * @author Yucchi */ public class Euclidean_Algorithm { public static void main(String[] args) { if (args.length != 2) { System.err.println("えらー (゜´Д`゜) 自然数を二つ入力してね。"); System.exit(0); } int x = java.lang.Integer.parseInt(args[0]); int y = java.lang.Integer.parseInt(args[1]); if (x < 0 || y < 0) { System.err.println("えらー (゜´Д`゜) 自然数を二つ入力してね。"); System.exit(0); } if (x < y) { y ^= x; x ^= y; y ^= x; } System.out.println(args[0] + " と " + args[1] + " の最大公約数は " + gcd(x, y) + " だよね。"); } private static int gcd(int x, int y) { return y == 0 ? x : gcd(y, x % y); } } |
非常にシンプルで解りやすいですね。
せっかくだからデバッグ実行させてプルグラムの流れを確認してみよう。
変数 x , y の値に注目です。
main() メソッドの引数二つを整数とし、大きさを比較し計算処理のため必要に応じて値を入れ替え、
再帰メソッドで答えが出るまで(再帰のループから抜ける条件になるまで)ひたすらぐるぐる回るってかんじ。
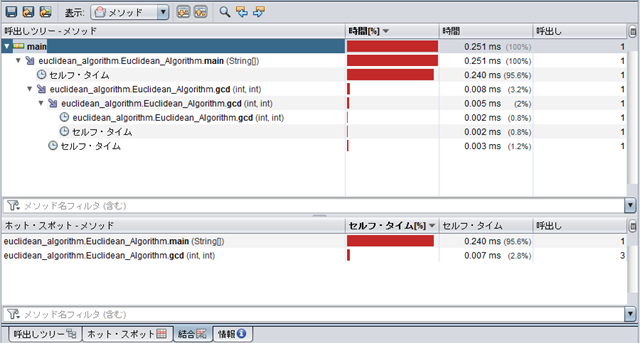
ユークリッドの互除法ってシンプルだけど良く考えられた素晴らしいものですね。
最後にすでにお気付きの方もいると思うのですが上記プログラムはちょっと手抜きの部分があります。
目的がユークリッドの互除法を試してみるということなのでご容赦のほどを(^_^;
ちなみに java.lang.NumberFormatException が・・・・・・です。(本当は忘れていたことは内緒です)

TAGS: Java |
2013年1月3日4:58 AM |
Java
再帰アルゴリズムの覚え書きの続きです。
再帰アルゴリズム その1
今回も、非効率的かつ非現実的な例題を利用して再帰アルゴリズムを理解していきましょう。
今回はフィボナッチ数列の特定項の値を求めるプログラムです。
フィボナッチ数列とは簡単に説明すると
F1 = 1
F2 = 1
F3 = 2
・
・
・
Fn = F(n – 2) + F(n – 1)
ただし、n = 1 または n = 2 のとき F(n) = 1 となる数列のことである。
つまり、1, 1, 2, 3, 5, 8, … と続く数列で、 隣り合う2つの数を足し算すると、その上位の数になる数列です。
参考までに、フィボナッチ数は、ちょうど800年前に刊行された「算盤の書」(1202年)の中の有名な「兎の問題」から生まれました。
これをプログラムにするにはどうしたらいいでしょうか?
数学的手法でいくか?ループ文で和を取り値を入れ替えながら?
面倒なのでここは再帰アルゴリズムを使いましょう。(^_^;
計算処理負荷が非常に大きいことは秘密にしておきましょう。(ヲヒ
とりあえずサクッと作ってみたのでデバッグ実行させてプログラムの流れを確認してみましょう。
| jp\yucchi.fibonacci.number.FibonacciNumber.java |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
package jp.yucchi.fibonacci.number; /** * * @author Yucchi */ public class FibonacciNumber { private static final int TARGET = 5; private static int ans; public static void main(String[] args) { ans = fib(TARGET); System.out.println("フィボナッチ数列第 " + TARGET + " は " + ans + " です。"); } private static int fib(int n) { if (n == 1 || n == 2) { return 1; } else { ans = fib(n - 2) + fib(n - 1); return ans; } } } |
上記のプログラムをデバッグ実行させます。
変数、n , ans の値、再帰呼び出し及び処理から戻ってくる時のプログラムの流れをしっかり確認してくださいませ。
しっかり確認できましたでしょうか?
概略図を作って流れを考察してみます。
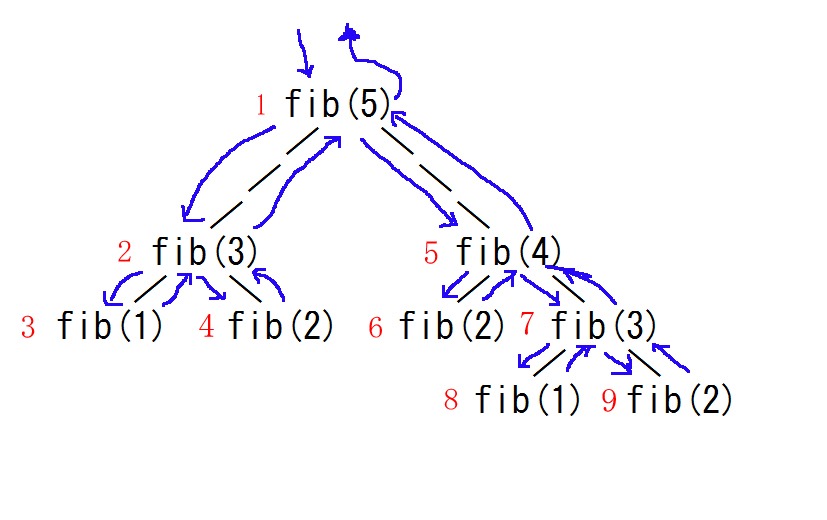
fib(5) から fib(5 – 2) そして fib(3 – 2)
処理を終え fib(5 – 2) に戻り次の fib(3 –1)
処理を終え fib(5 – 2) に戻り fib(5 – 2) の処理を終え fib(5) に戻る
そして fib(5 –1) へ、そして fib(4 – 2) へ、処理を終えて fib(5 – 1) へ戻る
次の fib(4 – 1) へ、そして fib(3 – 2) へ、処理を終えて fib(4 – 1) へ戻る
そして fib(3 – 1) へ、処理を終えて fib(4 – 1) へ戻る、処理を終えて fib(5 – 1) へ戻る、処理を終えて fib(5) に戻る
これでやっと呼び出し元に計算処理を結果を返せるって仕組みです。
あ~、しんど (~_~;)
再帰アルゴリズムってプログラムだとシンプルだけど流れを考えるとしんどいですね。
えっ?私だけ?
まぁ、いいか。
ちなみに再帰アルゴリズム使わないプログラムは下記のようになります。
| jp.yucchi.fibonacci.number2.FibonacciNumber2.java |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
package jp.yucchi.fibonacci.number2; /** * * @author Yucchi */ public class FibonacciNumber2 { private static final int TARGET = 5; public static void main(String[] args) { System.out.println("フィボナッチ数列第 " + TARGET + " は " + fib(TARGET) + " です。"); } private static int fib(int n) { int x = 1; int y = 1; for (int i = 2; i < TARGET; i++) { int z = x + y; y = x; x = z; } return x; } } |
さて、どちらが効率いいですか?

TAGS: Java |
2013年1月2日4:56 AM |
Java
再帰アルゴリズムについてちょっとしたメモを残しておきます。
まず再帰とは、あるものについて記述する際に、記述しているものそれ自身への参照が、その記述中にあらわれることをいうらしいです。
日本語って難しいですね。
プログラムを組む上でコーディングテクニックについては自分と同じ(自分自身)をある条件が満たされるまで呼び出し続けることのようです。
これって for 文もしくは while 文でもいけそうですね。
とりあえず非効率的かつ非現実的ではありますが 3 の階乗値を求めるプログラムを作ってみましょう。
| jp.yucchi.recursion.example.RecursionExample.java |
|
|
package jp.yucchi.recursion.example; /** * * @author Yucchi */ public class RecursionExample { private static final int TARGET = 3; public static void main(String[] args) { System.out.println("n の階乗値は " + fact(TARGET) +" です。"); } private static int fact(int n) { return n == 0 ? 1 : n * fact(n - 1); } } |
非常にシンプルです。
10 行目の標準出力処理の中にある fact(TARGET) メソッドで再帰メソッドを呼び出してます。
再帰メソッドが 13 行目の fact(int n) です。
14 行目から条件次第で再び呼び出されます。
全ての処理が帰ってきてから標準出力に fact(TARGET) の戻り値が出力されます。
これだったらループ文でも大差ないだろうと思った あ・な・た 正解です。(^_^;
しかし、この再帰アルゴリズムは奥が深いんです。
そのことはまた今度ってことで今回はこのシンプルなプログラムの流れをデバッガを使い確認してみます。
上記のプログラムのままでもいいのですが、ちょっと解りやすくするために下記のように変更します。
| jp.yucchi.recursion.example.RecursionExample.java |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
package jp.yucchi.recursion.example; /** * * @author Yucchi */ public class RecursionExample { private static final int TARGET = 3; public static void main(String[] args) { System.out.println("n の階乗値は " + fact(TARGET) +" です。"); } private static int fact(int n) { int temp = n == 0 ? 1 : n * fact(n - 1); return temp; } } |
それではプログラムの流れを変数 n , temp を確認しながらご覧ください。
どうですか?
処理が最初の呼び出し元に戻るまで追うことができましたでしょうか?
コードはすっきりとなってるけどプログラムの流れはけっこう追っていくのは大変です。
論理的に考えて組んでしまえばこのかったるい処理はコンピューターがやってくれるので非常に便利です。
今回は再帰アルゴリズムの基本中の基本のメモでした。
TAGS: Java |
2013年1月1日4:42 PM |
General
あけましておめでとうございます。
どうか本年も暖かい、もしくは生暖かい目で見守ってください。(^_^)
2013年はクラウディアさんと、ひときわ光り輝いている巨人の星をめざします。(ヲヒ

これだけだとさみしいので翻訳ソフトで英語にしてみた。
I congratulate you opening.
Please watch by a warm or lukewarm eye if you please this year also. (^_^)
I will aim at the star of the giant who is shining particularly with Claudia in 2013. (ヲヒ)
2013年1月1日12:14 AM |
新しい記事 »







