2013
Windows
ちょっと訳あって Windows 8 のパソコンでシステムのバックアップと復元を繰り返すという事態に陥った。
そもそも、Windows 8 対応のバックアップソフトで便利に使えるはずのものが私の環境ではことごとく何かしらの不具合がでる。
しかたないから標準搭載のバックアップシステムを使うこととした。
ところがそれで思わぬトラブルに遭遇した。
何回かバックアップと復元を繰り返し、バックアップしようとしたところ
バックアップに失敗しました。
ディスク領域が不足しているため、保存場所にボリュームのシャドウ コピーを作成できません。バックアップするすべてのボリュームについて、シャドウ コピーの作成に必要な最小限のディスク領域が利用可能であることを確認してください。これは、バックアップの保存先と、バックアップに含まれるボリュームの両方について行う必要があります。最小要件: 500 MB 未満のボリュームに対して 50 MB の空き領域、500 MB を超えるボリュームに対して 320 MB の空き領域が必要です。推奨事項: ボリュームのサイズが 1 GB を超える場合、各ボリュームについて、少なくとも 1 GB の空きディスク領域が必要です。
このようなエラーが表示されました。
何で?
バックアップ先のドライブ余裕しゃくしゃく釈由美子なんだけどなぁ・・・
試しにバックアップ先を変えても駄目。
よく読んでみるとバックアップ元のドライブにも空きが必要となってる。
システムで予約済みパーティションとシステムドライブだけしか選択してないし、さっきまでなんともなかったので不思議だ。
泣きたい気分になってきたが困ったときのグーグル先生に聞いてみたらありましたよ。
復元完了したばかりの状態ではシステムで予約済みパーティションに以前の環境のファイルが暫くのあいだ残るようです。
これが消去されない期間は上記のエラーメッセージのとおりになるようです。
私の環境ではシステム予約済みパーティションが 350MB あって空きが 9% しか無い状態になってました。
3,40 分後に調べてみたところ 27% まで復活していたのでこの問題は解決し、無事にバックアップできるようになりました。
めでたし!めでたし(^^)
まぁ、普通は復元とバックアップを繰り返すようなことはないからこのようなことはめったに起こらないでしょう。
でも、これってバグじゃないのか?
TAGS: Windows |
2013年2月6日10:37 PM |
Java
実行可能JARファイルが Java 7 になってから動かなくなってがっかりしていたが Windows 8 Pro , Java 7 u11 で動くことを確認!
いつから動くようになったのかは不明です。
また、Windows 7 での確認はまだしていません。
これで過去に作った自分専用の Java アプリが使えます。(^^)
そう言えばこの件をネットで調べていたとき同じように Java 7 で動かなくなって弱ってる人を発見しました。
早速教えてあげようと思ったがどこのサイトだったか記憶にない(^^;
TAGS: Java |
2013年1月30日5:10 PM |
Movie
おもしろかった(^^)
いつもながらのコンビの良さに安心できる。
しかし今回の作品は何故JがKにスカウトされる運命にあったか
KとJの過去に迫る作品となっていた。
ここでそれを語るとネタバレになるからやめておこう。
そうそう、Kは日本の缶コーヒーBOSSのコマーシャルやってるのに
コーヒーの味を「動物の死骸みたいな味だ」といっているのは笑えた。
「当たり前よ、今朝挽いた(轢いた)ばかり」といった返しでなりったってるけどちょっときついジョークですね。
細かい笑いの仕掛けがいたるところにあるので楽しめます。
大人が楽しめるようなラブストーリーではないが子供心を忘れていない大人に是非ご覧になっていただきたい。
あれっ?
チョコレートミルクが無性に飲みたくなってきたのは何故だ!
TAGS: Movie |
2013年1月19日8:24 PM |
Movie
私は時代劇はあまり好きではないがチャンバラは好きだ。
チャンバラという言い方は不適切だな。
格好いい派手な殺陣が好きだ。
最近殺陣が話題になるような時代劇は無かったと思う。
この映画で評論家が殺陣が斬新で素晴らしいと褒めていた。
出演者達もそうそうたるメンバーなのに演じ方とか褒めずに殺陣を褒めていた。
そこでレンタル開始されたので借りて見たところ素晴らしかった。
これは監督のこだわりだろう。
いい意味でこの殺陣だけでもこの映画は成立するといっても過言ではないだろう。
ただし、本格的時代劇ファンにとってはただのB級映画かもしれない。
もともと少年ジャンプに連載されていた漫画が原作なので大人向けのストーリーではない。
それが故に安心して楽しめる。
私は原作を読んでないので映画のストーリーを評価できないがそれでも楽しめた。
続編が作られたら必ず見てみたい作品である。
TAGS: Movie |
2013年1月9日7:23 PM |
Java
Java で Nクイーン問題 nQueens Problem をプログラミングしてみました。
まず Nクイーン問題とは何か?
ネットでググってみると8クイーン問題ってのがよくとりあげられてます。
Nクイーン問題とはそれを一般化したようです。
では8クイーン問題から調べていきましょう。
8クイーン問題では、王妃(クイーン)8個が用意されています。
チェス盤のサイズは王妃(クイーン)と同じ数とします。
8クイーンでは縦、横8マスです。
そのチェス盤に全ての王妃(クイーン)を配置します。
ただし、それぞれの王妃(クイーン)の利き筋には配置できません。(縦、横、斜めの4ライン)
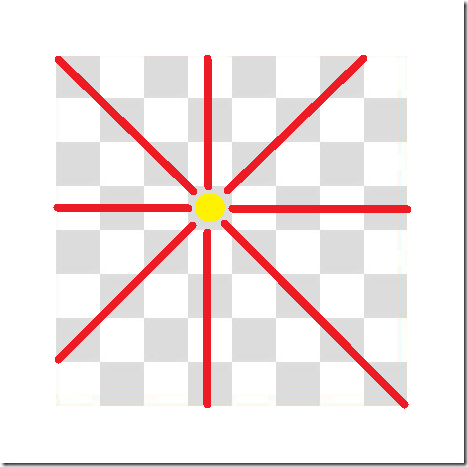
以上の条件を全て満たす王妃(クイーン)の配置パターン及び総数を求めるものです。
それではどうやって解を導き出したらいいのか考えてみることにします。
8個の王妃(クイーン)を全ての組み合わせに配置して上記の条件をクリアするかを確認すればいいだけのことですね。
しかし、その方法だと 8 X 8 = 64 マスあるから
64 X 63 X 62 X 61 X 60 X 59 X 58 X 57 = 178,462,987,637,760 通りもあることになります。
ちょっと多いですね。
王妃(クイーン)の数が大きくなった時のことを考えたら厳しいです。
しかし、全ての組み合わせを調べる必要はなさそうです。
何故なら、同じ列、行に王妃は配置できないからです。
縦、横の利き筋の条件を考慮した結果、各列、行には王妃(クイーン)は 1 個だけしか配置できない!
よって、 8! = 40,320 通りまで激減させることができる。
あと斜めの利き筋2つを利用すれば計算処理はもっと少なくなるだろう。
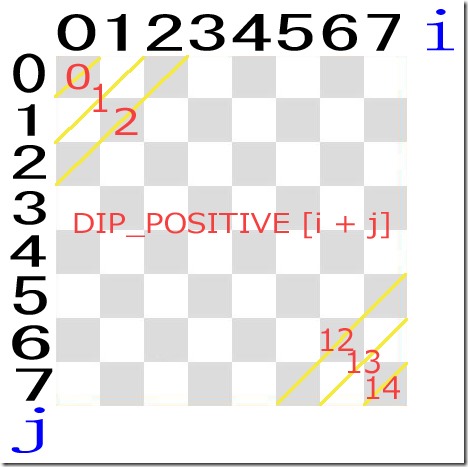
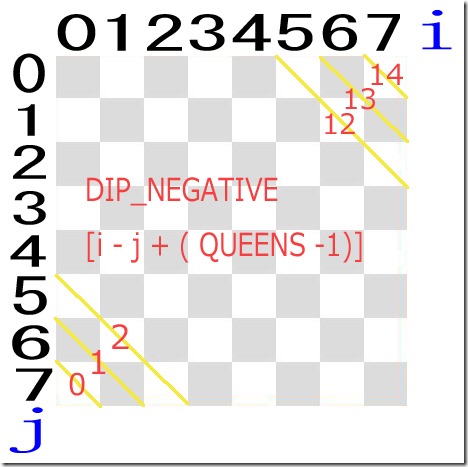
以上のことを考慮した上で次のようなプログラムを作ればいいかもしれない。
private static void trySet(int i) {
for (王妃の数だけループ) {
if (利き筋から外れていれば) {
王妃 i 列 j 行に配置
if (i == (王妃8個配置できたら) {
トータルパターン数をカウントアップ
盤面を表示
}else {
王妃の利き筋(行、斜め)をセット
次の列を配置(再帰 trySet(i + 1))
王妃の利き筋(行、斜め)を解除
}
}
}
}
ってことで作ってみました。
ただ、デバッガでプログラムの流れを追うために王妃(クイーン)の数は 4 としました。
もちろん、王妃(クイーン)の数は一般化できるようにしてあります。
| nqueensproblem.NQueensProblem.java |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
package nqueensproblem; /** * * @author Yucchi */ public class NQueensProblem { // 王妃数 private static final int QUEENS = 4; // 王妃の配置位置 private static final int [] VERTICAL = new int [QUEENS]; // 行に王妃が配置されてるかチェック用 private static final boolean [] HORIZONTAL = new boolean [QUEENS]; // 右45度斜めラインに王妃が配置されているかチェック用 private static final boolean [] DIP_POSITIVE = new boolean [QUEENS * 2 -1]; // 左45度斜めラインに王妃が配置されているかチェック用 private static final boolean [] DIP_NEGATIVE = new boolean [QUEENS * 2 - 1]; // 安全 private static final boolean SAFE = false; // 危険 private static final boolean OUT = true; // トータルパターン数 private static int counter; public static void main(String[] args) { trySet(0); if(counter < 1){ System.out.println("配置不可能でした。"); }else{ System.out.println(counter + " パターン配置可能でした。"); } } // 全ての可能な王妃の配置位置を取得、そしてトータルパターン数も取得する。 private static void trySet(int i) { for (int j = 0; j < QUEENS; j++) { // 行 ( j )、/右45度斜めライン ( i + j )、\左45度斜めライン (i - j + ( QUEENS -1 )) 配置チェック if (HORIZONTAL [j] == SAFE && DIP_POSITIVE [i + j] == SAFE && DIP_NEGATIVE [i - j + ( QUEENS -1)] == SAFE) { VERTICAL [i] = j; // 王妃 i 列 j 行に配置 if (i == ( QUEENS -1)) { // 王妃の配置完了 counter++; // トータルパターン数カウンター printBoard(); // 盤面を表示 }else { // 王妃の利き筋(行、斜め)をセット HORIZONTAL [j] = DIP_POSITIVE [i + j] = DIP_NEGATIVE [i - j + ( QUEENS -1)] = OUT; // 次の列を配置 trySet(i + 1); // 王妃の利き筋(行、斜め)を解除 HORIZONTAL [j] = DIP_POSITIVE [i + j] = DIP_NEGATIVE [i - j + ( QUEENS -1)] = SAFE; } } } } // 全ての可能な王位配置位置を出力 ●が王妃が置かれた場所である。 private static void printBoard() { System.out.println("第 " + counter + " パターン"); for (int i = 0; i < QUEENS; i++) { for (int j = 0; j < QUEENS; j++) { System.out.printf("%s", j == VERTICAL [i] ? "● " : "□ "); } System.out.println(); } System.out.println(); } } |
さて、理屈やコードだけでは解りにくいかもしれないのでこのプログラムの流れをデバッグ実行して確認してみます。
デバッグウィンドウやウォッチポイントの変数の値を確認しながらごらんくださいませ。
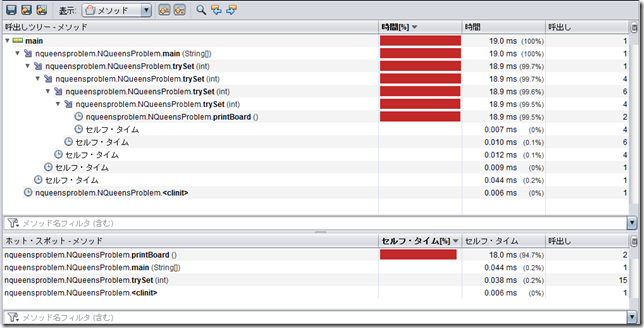
プログラムの流れを見ていると人間の思考原理に非常に良く似ていますね。
とりあえず順番に試してみる。
条件を考慮して無駄なことはせず作業量を減らす。
途中で駄目だと判断できたら戻って次のパターンからやり直す。
それの繰り返しで処理を完了する。
こういったアルゴリズムはバックトラック法って言われているようです。
深さ優先探索アルゴリズムですね。
試行錯誤的に解を探し出すタイプの問題に有効です。
つまり、基本的に全ての選択肢を試してみるしか無い場合なんかには有効のようです。
いつ頃、誰が、どのような理由でこういったアルゴリズムを考えたのか?
考えた人を心から尊敬します。
ちなみに 8王妃問題としてプログラムを実行したい場合は上記プログラムの 9 行目の
private static final int QUEENS = 4; // 王妃数
王妃数を 8 に変更してください。
任意の王妃数をこれによって設定できますがあまり王妃数を大きくすると計算量が指数関数的に増加するでしょうからほどほどに(^_^;

再帰アルゴリズムについてはこちらで簡単な覚え書きを残してあります。
再帰アルゴリズム その1
再帰アルゴリズム その2
ユークリッドの互除法 Euclidean Algorithm
ハノイの塔 Tower of Hanoi
TAGS: Java |
2013年1月5日6:58 AM |
« 古い記事
新しい記事 »





